Solveeit Logo
Login

Question

Question: Find the number of integers $n$ such that $1 \leq n \leq 100$ and $n^2 + 3n + 2$ is divisible by 5....

Find the number of integers nn such that 1≤n≤1001 \leq n \leq 100 and n2+3n+2n^2 + 3n + 2 is divisible by 5.

Answer

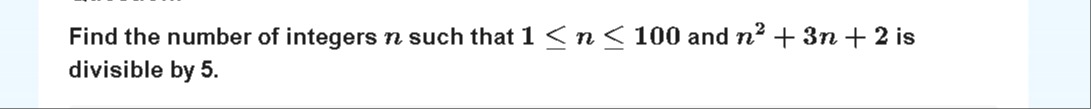
40

Explanation

Solution

The given expression is n2+3n+2n^2 + 3n + 2.
First, we factorize the quadratic expression:
n2+3n+2=(n+1)(n+2)n^2 + 3n + 2 = (n+1)(n+2)

For n2+3n+2n^2 + 3n + 2 to be divisible by 5, the product (n+1)(n+2)(n+1)(n+2) must be divisible by 5.
Since 5 is a prime number, for a product of two integers to be divisible by 5, at least one of the integers must be divisible by 5.
So, either (n+1)(n+1) is divisible by 5, or (n+2)(n+2) is divisible by 5.

We can analyze this using modular arithmetic:
The expression (n+1)(n+2)(n+1)(n+2) must be congruent to 0(mod5)0 \pmod{5}.

Let's check the possible remainders of nn when divided by 5:

  1. If n≡0(mod5)n \equiv 0 \pmod{5}:
    (n+1)(n+2)≡(0+1)(0+2)≡1⋅2≡2(mod5)(n+1)(n+2) \equiv (0+1)(0+2) \equiv 1 \cdot 2 \equiv 2 \pmod{5}. Not divisible by 5.
  2. If n≡1(mod5)n \equiv 1 \pmod{5}:
    (n+1)(n+2)≡(1+1)(1+2)≡2⋅3≡6≡1(mod5)(n+1)(n+2) \equiv (1+1)(1+2) \equiv 2 \cdot 3 \equiv 6 \equiv 1 \pmod{5}. Not divisible by 5.
  3. If n≡2(mod5)n \equiv 2 \pmod{5}:
    (n+1)(n+2)≡(2+1)(2+2)≡3⋅4≡12≡2(mod5)(n+1)(n+2) \equiv (2+1)(2+2) \equiv 3 \cdot 4 \equiv 12 \equiv 2 \pmod{5}. Not divisible by 5.
  4. If n≡3(mod5)n \equiv 3 \pmod{5}:
    (n+1)(n+2)≡(3+1)(3+2)≡4⋅5≡4⋅0≡0(mod5)(n+1)(n+2) \equiv (3+1)(3+2) \equiv 4 \cdot 5 \equiv 4 \cdot 0 \equiv 0 \pmod{5}. Divisible by 5.
  5. If n≡4(mod5)n \equiv 4 \pmod{5}:
    (n+1)(n+2)≡(4+1)(4+2)≡5⋅6≡0⋅1≡0(mod5)(n+1)(n+2) \equiv (4+1)(4+2) \equiv 5 \cdot 6 \equiv 0 \cdot 1 \equiv 0 \pmod{5}. Divisible by 5.

Thus, n2+3n+2n^2+3n+2 is divisible by 5 if and only if n≡3(mod5)n \equiv 3 \pmod{5} or n≡4(mod5)n \equiv 4 \pmod{5}.
These two conditions are mutually exclusive, as an integer cannot leave both a remainder of 3 and a remainder of 4 when divided by 5.

Now we need to count the number of integers nn such that 1≤n≤1001 \leq n \leq 100 and nn satisfies one of these conditions.

Case 1: n≡3(mod5)n \equiv 3 \pmod{5}
These integers are of the form 5k+35k+3.
For 1≤n≤1001 \leq n \leq 100:
1≤5k+3≤1001 \leq 5k+3 \leq 100
Subtract 3 from all parts:
1−3≤5k≤100−31-3 \leq 5k \leq 100-3
−2≤5k≤97-2 \leq 5k \leq 97
Divide by 5:
−25≤k≤975-\frac{2}{5} \leq k \leq \frac{97}{5}
−0.4≤k≤19.4-0.4 \leq k \leq 19.4
Since kk must be an integer, kk can take values from 0,1,2,…,190, 1, 2, \dots, 19.
The number of such values of kk is 19−0+1=2019 - 0 + 1 = 20.

Case 2: n≡4(mod5)n \equiv 4 \pmod{5}
These integers are of the form 5k+45k+4.
For 1≤n≤1001 \leq n \leq 100:
1≤5k+4≤1001 \leq 5k+4 \leq 100
Subtract 4 from all parts:
1−4≤5k≤100−41-4 \leq 5k \leq 100-4
−3≤5k≤96-3 \leq 5k \leq 96
Divide by 5:
−35≤k≤965-\frac{3}{5} \leq k \leq \frac{96}{5}
−0.6≤k≤19.2-0.6 \leq k \leq 19.2
Since kk must be an integer, kk can take values from 0,1,2,…,190, 1, 2, \dots, 19.
The number of such values of kk is 19−0+1=2019 - 0 + 1 = 20.

Since the two cases are mutually exclusive, the total number of integers nn is the sum of the counts from Case 1 and Case 2.
Total number of integers = 20+20=4020 + 20 = 40.

Alternatively, we can observe that in any block of 5 consecutive integers (e.g., 1,2,3,4,51,2,3,4,5 or 6,7,8,9,106,7,8,9,10), there will be exactly one integer nn such that n≡3(mod5)n \equiv 3 \pmod{5} and exactly one integer nn such that n≡4(mod5)n \equiv 4 \pmod{5}.
The range 1≤n≤1001 \leq n \leq 100 contains 100 integers.
Since 100=20×5100 = 20 \times 5, there are 20 such blocks of 5 integers.
Each block contributes 2 integers for which n2+3n+2n^2+3n+2 is divisible by 5.
So, the total number of integers is 20×2=4020 \times 2 = 40.

The final answer is 40\boxed{40}.