Question

Find the number of images.

Answer 1

Multiple images are formed when two mirrors are kept inclined to each other. The number of images depends on the angle between them. Since the image formed by a plane mirror is virtual, it is formed at the back of the mirror and is at the same distance from the mirror as the object.

Formula used:
$\text{n = }\dfrac{{{360}^{\text{o}}}}{\text{A}}\text{ - 1}$ (When $\dfrac{{{360}^{\text{o}}}}{\text{A}}$ is even) - (1)
$\text{n = }\dfrac{\text{36}{{\text{0}}^{\text{o}}}}{\text{A}}$ (When $\dfrac{{{360}^{\text{o}}}}{\text{A}}$is odd) - (2)
$\text{n = }\dfrac{{{360}^{\text{o}}}}{\text{A}}\text{ - 1}$(When object is kept symmetrically) - (3)
$\text{n = }\dfrac{\text{36}{{\text{0}}^{\text{o}}}}{\text{A}}$(When object is kept asymmetrically) -(4)

Complete step-by-step answer:
A plane mirror forms a single, virtual and erect image of the same size as the object. The image is laterally inverted. But when two mirrors are kept together inclined at an angle, more than two images are formed depending on the angle between them. This happens because the rays coming from each mirror get reflected multiple times between both mirrors and new images of the old images are created.
No of images formed, $\text{n}$when two mirrors are inclined at angle $\text{A}$is given by-
$\text{n = }\dfrac{{{360}^{\text{o}}}}{\text{A}}\text{ - 1}$ (When $\dfrac{{{360}^{\text{o}}}}{\text{A}}$ is even) - (1)
$\text{n = }\dfrac{\text{36}{{\text{0}}^{\text{o}}}}{\text{A}}$ (When $\dfrac{{{360}^{\text{o}}}}{\text{A}}$is odd) - (2)
$\text{n = }\dfrac{{{360}^{\text{o}}}}{\text{A}}\text{ - 1}$(When object is kept symmetrically) - (3)
$\text{n = }\dfrac{\text{36}{{\text{0}}^{\text{o}}}}{\text{A}}$(When object is kept asymmetrically) -(4)

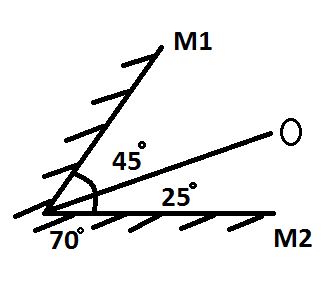
The in the given figure, the object is more inclined towards $\text{M2}$which means that it is kept asymmetrically between the mirrors, so using eq (4) to calculate the number of images formed by both mirrors, we get,

& \text{n = }\dfrac{360}{70} \\\ & \Rightarrow \text{ n = 4}\text{.14 } \\\ \end{aligned}$$ The integral part of $$\text{n}$$ is the total number of images formed which is 4. Hence, 4 images of the object were formed by both mirrors. **Note:** The rays falling on the mirror from the object are parallel to each other. They come from infinity and reflect back to infinity. It follows the laws of reflection which states that the angle of incidence is equal to the angle of reflection,$$\text{i = r}$$and incident ray, normal ray and the reflected ray lie in the same plane.