Question

Find the number of critical points of the function $\dfrac{2}{3}\sqrt{{{x}^{3}}}-\dfrac{x}{2}+\int_{1}^{x}{\left( \dfrac{1}{2}+\dfrac{\cos 2t}{2}-\sqrt{t} \right)dt}$ in the interval $\left[ -2\pi ,2\pi \right]$.
[a] 2
[b] 6
[c] 4
[d] 8

Answer 1

Use the fact that if f(x) is a differentiable function, then the critical points are the roots of the equation $f'\left( x \right)=0$. Use first fundamental theorem of calculus which states that $A'\left( x \right)=\dfrac{d}{dx}\int_{a}^{x}{f\left( t \right)dt}=f\left( x \right)$ and hence prove that the critical roots are the roots of the equation $\cos 2x=0$. Use the fact that if $\cos x=\cos y$, then $x=2n\pi \pm y,n\in \mathbb{N}$. Hence find the critical roots in the interval $\left[ -2\pi ,2\pi \right]$

Complete step-by-step solution:
We have been given a function and let us take it as $f\left( x \right)=\dfrac{2}{3}\sqrt{{{x}^{3}}}-\dfrac{x}{2}+\int_{1}^{x}{\left( \dfrac{1}{2}+\dfrac{1}{2}\cos 2t-\sqrt{t} \right)dt}$
We know that if $f\left( x \right)$ is a differentiable function, then the critical roots are given by the equation $f'\left( x \right)=0$.
Hence differentiating both sides, we have
$f'\left( x \right)=\dfrac{2}{3}\dfrac{d}{dx}\left( {{x}^{\dfrac{3}{2}}} \right)-\dfrac{1}{2}\dfrac{dx}{dx}+\dfrac{d}{dx}\left( \int_{1}^{x}{\left( \dfrac{1}{2}+\dfrac{\cos 2t}{2}-\sqrt{t} \right)} \right)$
We know that $A'\left( x \right)=\dfrac{d}{dx}\int_{a}^{x}{f\left( t \right)dt}=f\left( x \right)$(This is the first fundamental theorem of calculus)
Hence, we have
$f'\left( x \right)=\dfrac{2}{3}\times \dfrac{3}{2}\sqrt{x}-\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{\cos 2x}{2}-\sqrt{x}=\dfrac{\cos 2x}{2}$
Hence the critical roots of f(x) are the roots of the equation $\dfrac{\cos 2x}{2}=0$
Multiplying both sides by 2, we get
$\cos 2x=0$
We know that $\cos \dfrac{\pi }{2}=0$
Hence, we have
$\cos 2x=\cos \dfrac{\pi }{2}$
We know that $\cos x=\cos y\Rightarrow x=2n\pi \pm y,n\in \mathbb{N}$
Hence, we have
$2x=2n\pi \pm \dfrac{\pi }{2},n\in \mathbb{N}$
Dividing both sides by 2, we get
$x=n\pi \pm \dfrac{\pi }{4},n\in \mathbb{N}$
Put $n=0,1,2,-1,-2$, we get
$x=\pm \dfrac{\pi }{4},\pm \dfrac{3\pi }{4},\pm \dfrac{5\pi }{4},\pm \dfrac{7\pi }{4}$
Hence the number of critical points in the interval $\left[ -2\pi ,2\pi \right]$ is 8
Hence option [d] is correct.

Note: [1] Note that we can directly find the number of solutions of the equation $\cos 2x=0$ in the interval $\left[ -2\pi ,2\pi \right]$ using graph paper.
We draw the graph of cos2x as follows

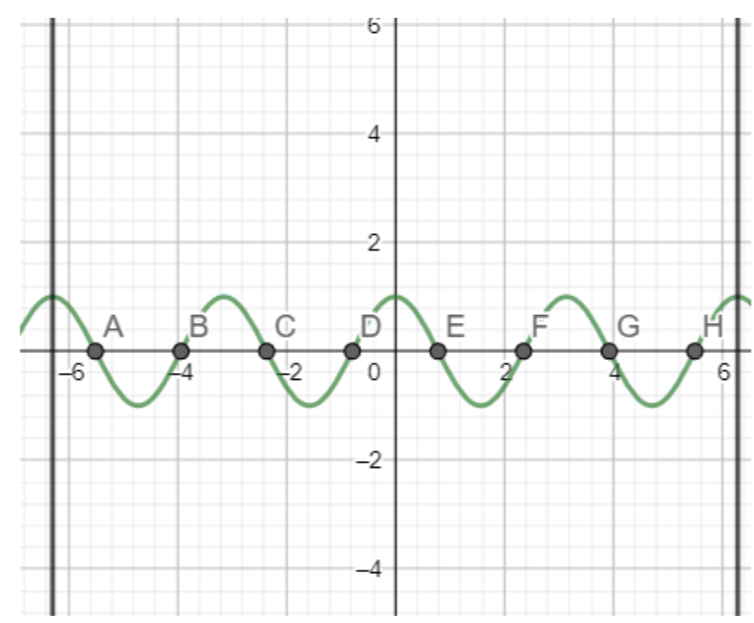
As is evident from the graph that there are 8 solutions in the interval $\left[ -2\pi ,2\pi \right]$
Hence option [d] is correct.