Question
Question: Find the number of all the integral of the inequality \[\dfrac{{({x^2} + 2)(\sqrt {{x^2} - 16} )}}{{...
Find the number of all the integral of the inequality (x4+2)(x2−9)(x2+2)(x2−16)⩽0.
Solution
Consider only those terms which affect the inequality sign less than equal to. First we change the denominator sign on the right side and then we will solve the equation.
Complete step by step answer:
(1) Given inequality is (x4+2)(x2−9)(x2+2)x2−16⩽0
Since, LHS of inequality is negative but terms (x2+2) and (x4+2) are always positive for all value of x.
(2) On taking (x2+2) and (x4+2) on RHS, we have
(x2−9)x2−16⩽0
(3) But x2−16⩾0always
∴forx2−9x2−16 to be negative
x2−16⩾0,x2−9⩽0
Implies that x2−9⩽0
(4) Hence from above we got two inequalities
x2−16⩾0,x2−9⩽0
Solving separately by these two terms,
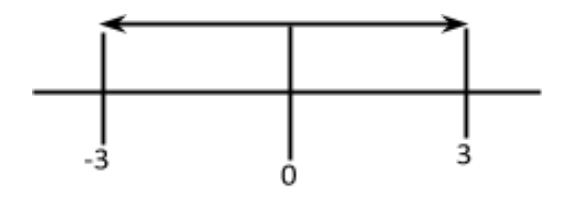
(5)x2−9⩽0
x2⩽9
x⩽3
−3<x<3
x∈(−3,3)
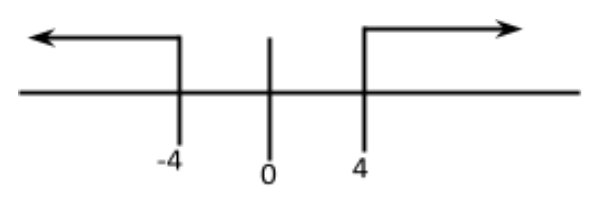
(6) Also,
x2−16⩾0
(7) On combining two solutions in number line
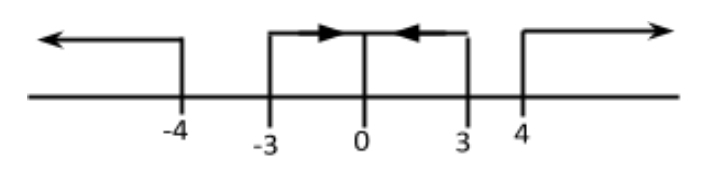
(8) There is no common region hence integral value of solution for given inequality is zero (ϕ).
Note: If f(x)⩽g(x)on the interval [a,b], then the integral of f(x) is less than or equal to the integral of g(x)on the interval [a,b]. As a special case, if m⩽f(x)⩽M on [a,b], then the integral of f(x) is between m(b−a) and M(b−a).
