Question

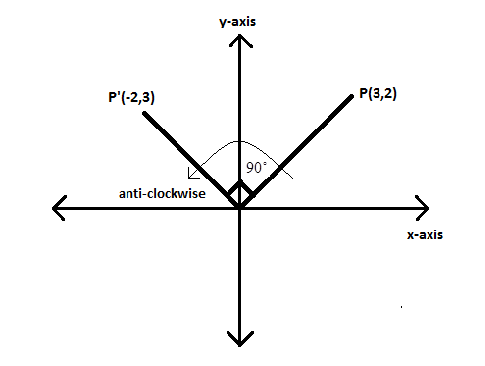
Find the new coordinates of a point P (3, 2) if it is rotated 90 degrees in counterclockwise direction with respect to the origin
A. (-2,3)
B. (-2,-3)
C. (-3,3)
D. (-3,2)
E. (-3,-2)

Answer 1

When a point is rotated through ${90^ \circ }$ about the origin in the clockwise direction then the point $M(h,k)$ takes the image $M'(k, - h)$ and when the point is rotated through ${90^\circ }$ about the origin in the counterclockwise direction then the point $M(h,k)$ takes the image $M'( - k,h)$ . In this question we are given a point which is rotated by ${90^ \circ }$ in counterclockwise direction so we will find the new coordinate after rotation about the origin.

Complete step by step solution:
Given the point whose new coordinate is to be found is $P\left( {3,2} \right)$
Let the new coordinate of point after the rotation be $P'$
Now we know when the point is rotated through ${90^ \circ }$ about the origin in the counterclockwise direction then the point $M(h,k)$ takes the image $M'( - k,h)$ .
Now since after rotations of the point $M(h,k)$ takes the image $M'( - k,h)$ , hence we can write the new coordinate of the point $P$ will be

$$\because M(h,k) \to M'( - k,h) \\\ \therefore P\left( {3,2} \right) \to P'\left( { - 2,3} \right) \\\$$

Therefore the new coordinates of a point P (3, 2) if it is rotated 90 degrees in counterclockwise direction with respect to the origin will be $P'\left( { - 2,3} \right)$

Option A is correct.

Note: In the coordinate of a point $A(h,k)$ , $h$ means a point on the x-axis of a two dimensional graph and $k$ is a point on the y-axis of a two dimensional graph.
We can also solve this problem by plotting the point $P\left( {3,2} \right)$ on a two dimensional graph and then rotating that point by ${90^ \circ }$ about the origin in the counterclockwise direction.