Question

Find the net electric field at point B where both charges are positive and equal. Point B is at the midpoint of line joining both charges.

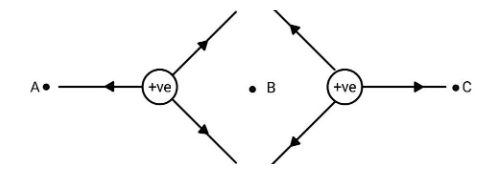
(A) Maximum
(B) Minimum
(C) Zero
(D) None

Answer 1

Electric field is a region in which charged particles experience force on them. Electric charges, positive as well as negative, produce electric fields around them. So, there will be electrostatic force acting in between these two charges. The force is given by the Coulomb’s Law and the value of the electric field is given as force per unit charge. So, consider Coulomb's law and find the electric field at point B.

Complete step by step answer:
Let us consider two particles, one at the origin having charge ${q_1}$ and the other at some position vector ${\mathbf{r}}$ having charge ${q_2}$, this charge ${q_2}$ is a test charge.The force due to charge ${q_1}$ on charge ${q_2}$ is given by the Coulomb’s law as ${{\mathbf{F}}_{12}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_1}{q_2}}}{{{r^2}}}\widehat {\mathbf{r}}$, where $\widehat {\mathbf{r}}$ is the unit vector of the position. In terms of magnitude, it is given as $F = \dfrac{{{q_1}{q_2}}}{{4\pi {\varepsilon _0}{r^2}}}$.

Now, take the charge ${q_2}$ on the left-hand side, you will get, $\dfrac{F}{{{q_2}}} = \dfrac{{{q_1}}}{{4\pi {\varepsilon _0}{r^2}}}$. This quantity is defined as the electric field $E = \dfrac{{{q_1}}}{{4\pi {\varepsilon _0}{r^2}}}$ due to charge ${q_1}$. For a positively charged particle, the electric field points outward from the point of source and for a negatively charged particle, the electric field points inward towards the point of source.

Let us come back to our question. First consider the charge on the left-hand side. The electric field due to that particle at the point B will be given as ${E_L} = \dfrac{q}{{4\pi {\varepsilon _0}{r^2}}}$ where $q$ is the charge and the direction of the electric field will be towards right. If we denote the direction pointing towards right as $\widehat i$ then the direction point towards left will be $- \widehat i$. So, due to the left charged particle,
${E_L} = \dfrac{q}{{4\pi {\varepsilon _0}{r^2}}}\widehat i$

Now, consider the charged particle on the right-side, the electric field will be given as,
${E_R} = - \dfrac{q}{{4\pi {\varepsilon _0}{r^2}}}\widehat i$
If we apply the superposition theorem, the net electric field will be the sum of the electric fields due to both the charges. As you can notice that both cancel out after getting added and the net electric field at point B is zero.Therefore, the net electric field at point B is zero.

Hence, option C is correct.

Note: Remember that the electric field is defined as force per unit charge. This value of electric field can be found out using the Coulomb’s Law which states that the force between two charged particles is directly proportional to the charges and inversely proportional to the square of the distance between the charged particles. Also keep in mind that the electric field points radially outward in case of positive charge and points radially inward in case of negative charge.