Question

Find the net acceleration at the instant it leaves the hemisphere.

A. $g$
B. $\dfrac{g}{2}$
C. $g$
D. $\dfrac{g}{3}$

Answer 1

When answering this question, it's a good idea to draw a free body diagram. The normal force vanishes when the body is going to depart the hemisphere, hence N=0 is a key element to remember when solving this equation. At that point, the force on the hemisphere would be equivalent to the centripetal force.

Complete step by step answer:
Let us know about acceleration. In mechanics, acceleration is the rate at which an object's velocity changes with respect to time. The term "acceleration" refers to a quantity that is measured in vectors (in that they have magnitude and direction). The direction of an object's acceleration is determined by the orientation of the net force acting on it.

Before we begin to solve the problem that has been posed to us, let us review all of the criteria that have been provided.
Mass of the block $=$m, Radius$=$r

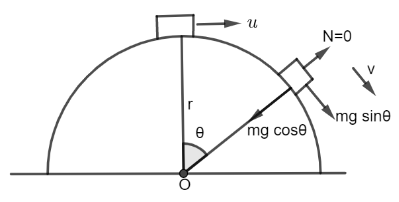
Assume $\theta$ is the angle at which it departs from the surface, and V is the speed at this point.By using force balance equation:
$mg\,\cos \theta - N = \dfrac{{m{V^2}}}{R}$
$\Rightarrow N = 0$
$\Rightarrow \dfrac{{{V^2}}}{R} = g\cos \theta$
Radial acceleration is defined as "the acceleration of the item along the radius, directed towards the centre" in a uniform circular motion.
${a_R} = g\,\cos \theta$

Tangential acceleration is a notion that is used to measure the change in tangential velocity of a point with a certain radius as time passes. The linear and tangential accelerations are the same, but the circular motion is caused by the tangential acceleration. The rate of change of the tangential velocity of the matter in a circular path is known as tangential acceleration.
${a_T} = g\,\sin \theta$
$\Rightarrow a = \sqrt {a_R^2 + a_T^2}$
$\Rightarrow a = \sqrt {{{(g\cos \theta )}^2} + {{(g\sin \theta )}^2}}$
$\therefore a = g$

So, option A is correct.

Note: In order to solve this problem there are some important points which we should keep on our fingertips. We should focus on Circular motion and acceleration regarding it like radial and tangential acceleration. By using this concept we got the value of acceleration as $g.$