Question
Question: Find the natural frequency of the system shown in the figure. The pulleys are smooth and massless. ...
Find the natural frequency of the system shown in the figure. The pulleys are smooth and massless.
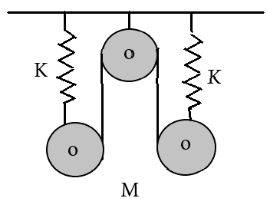
Solution
Hint : The springs of the system can be considered to be equivalent to two springs in parallel. The tension in each of the strings can be said to lift a quarter of the mass of the body attached to the pulley.
Formula used: In this solution we will be using the following formula;
keq=k1+k2 where keq is equivalent spring constant of two springs connected in parallel, and k1 and k2 are the spring constant of the individual springs.
ω=mk where ω is the natural frequency of a system of one spring attached to a mass.
Complete step by step answer:

Let us assume that a mass M was attached to the system as shown. At equilibrium, the tension in the springs and the strings T1...T4 are equal. Hence, T1...T4=T
Now, the equivalent spring constant of the system can be given as
Keq=K+K=2K
This is because, for two springs in parallel (i.e. independently attached to the same mass), the equivalent spring constant of the system is
keq=k1+k2 where keq is equivalent spring constant of two springs connected in parallel, and k1 and k2 are the spring constant of the individual springs.
Now, since a total tension of T1+T2+T3+T4=T+T+T+T=4T , then the mass carried by each spring is actually 4M .
These two implications signify that a spring is as though it has a spring constant of 2K , and carries only a mass of 4M .
Now, ω=mk where ω is the natural frequency of a system of one spring attached to a mass.
Hence, for the above, the natural frequency of the system would be
ω=4M2K=2K×M4
Hence,
ω=M8K .
Note:
For clarity, the natural frequency of a body is the frequency at which it will oscillate if it were displaced from equilibrium. Hence, a system does not only have a natural frequency only when it is oscillating. The existence of the system itself creates a natural frequency.
An application of it is to create or avoid resonance. Engineers calculate the natural frequencies of buildings, bridges, etc to ensure that nothing in the vicinity will allow the building to be set in resonance and will cause demolition of the building or bridge.
