Question
Question: Find the natural frequency of the system shown in the figure. The pulleys are smooth and massless. ...
Find the natural frequency of the system shown in the figure. The pulleys are smooth and massless.
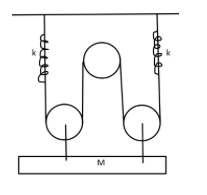
Solution
You can easily solve this question by first assuming that the mass M goes down by a distance x and then observing the effects on Tension in strings and springs and the displacement on pulleys, strings and both the springs, then comparing this to the condition in mean position.
Complete step by step answer:
We will be approaching the solution to the question exactly as described in the hint section of the solution to the question. First, let us consider the situation of equilibrium or mean position.
We can clearly see that there are 4 strings, which share equal tension, as the mass M is equally balanced. Hence, we can write:
4T=Mg
At mean position, displacements of both the springs can be assumed to be xo, hence, we can write:
kxo=T=4Mg, where k is the given spring constant of both the springs.
Let us now assume that the mass M goes down by a distance of x. Since the mass is balanced by the two lower pulleys, they both would need to move an equal distance to maintain the balance of the mass M. So, we can confidently say that if the mass M moves downwards by a distance x, both the lower pulleys will also go downwards by a distance of x .
We can see that one side of the string is shared by both of the lower pulleys, and thus, this side’s string cannot contribute to the movement of the pulleys downwards, so it needs to be compensated by the springs on the other sides. Hence, if both of the lower pulleys go down by a distance x, both of the springs will displace extra by a distance of 2x .
Also, we need to assume an acceleration a, against the motion.
Now, we can write:
Mg−4k(xo+2x)=Ma
We have already developed earlier that Mg=4kxo, using that here, we get:
−8kx=Ma
Or,
Frestorting=Ma=−(8k)x a=−(M8k)x
Comparing this to the general equation of SHM, we get:
ω=M8k
Frequency of SHM is:
f=2πω
Substituting the value of ω, we get:
f=π1M2k
Note: Many students commit mistakes and do not consider the tension that is on the passive part of the string, i.e. the part of string which is not contributing in the movement of the pulleys. Due to this tiny mistake, you can lose marks. Also, remember to compare the value of ω with the equation of acceleration and not the equation of force.
