Question
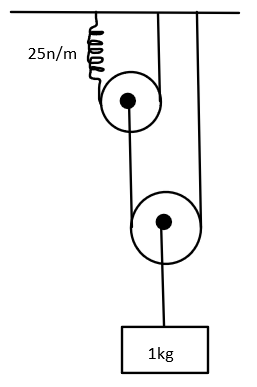
Question: Find the natural frequency of oscillation of the system as shown in the figure. Pulleys are massless...
Find the natural frequency of oscillation of the system as shown in the figure. Pulleys are massless and frictionless. Spring and string are also massless. (Take π2=10)
A) 2πHz
B) πHz
C) π10Hz
D) πHz
Solution
You can easily solve this question by considering how much each pulley, thus each string and thus the spring will move when the mass goes down by a length of x. Using this, you can write the force on the string as Fspring=−kxacting and use the same to find the frequency of oscillation.
Complete step by step answer:
We will approach the solution exactly as told in the hint section of the solution to the question.
Let’s first see how the force applied due to the mass of 1kg is being divided between the pulleys and among the strings and spring.
Let us assume that the force is F.
We can see that the lower pulley has two strings to support the weight. Hence, the force gets equally distributed between them. Thus, we can say that both sides now experience a force of magnitude of 2F.
Now, the upper pulley experiences a total force of 2F magnitude, which further gets equally distributed on both sides, thus, we can say that the spring and the string experience an equal force of magnitude 4F.
Now, we will check what happens when the body moves down by a distance x,
When the mass of 1kg goes down by a distance of x, the lower pulley also goes down by the same distance of x. Since one side of the string is fixed, it can not move down by the distance x, hence, the string attached to the upper pulley goes down by a distance of 2x. If it happens, the upper pulley would move down by a distance of 2x. Again, one side of the string is fixed, hence, spring will have to compensate for it by moving a distance of 4x.
Now, we have found out the force acting on the spring as well as the actual displacement of the spring when the mass goes down by a distance of x.
We can write it mathematically as
4F=−k(4x)
Further simplifying, we can write it as:
⇒F=−16kx
The value of spring constant (k) as given in the question is 25n/m
Substituting the value of spring constant here, we get:
⇒F=−(16×25)x
⇒F=−400x
Now, we can confidently say that the object performs SHM with ω=400=20rad/s
We already know that frequency can be given as
f=2πω
Substituting in the value of ω , we get
⇒f=2π20
Simplifying and then putting 10=π2(approximation) as told in the question, we get:
⇒f=πHz
Hence, the correct option is option (D).
Note:
Many students believe that if the object is moving down by a distance of x each string and spring will do the same, which is a completely wrong assumption and causes them to lose marks. Also, always remember that this is the best approach to solve such questions.
