Question
Question: Find the moment of inertia through the face diagonal of a cube. Edge length of a cube is \(a\) units...
Find the moment of inertia through the face diagonal of a cube. Edge length of a cube is a units.
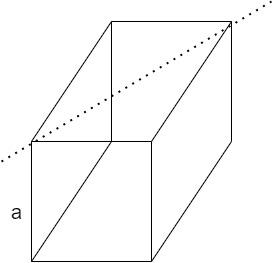
Solution
Moment of inertia of a body is defined as the tendency of the body to resist change in angular acceleration.
It is calculated for individual axis of rotations and depends on shape of the body because shape affects distribution of mass.
General formula: I=∑mi(ri)2
Where I= Moment of inertia around a particular axis
mi = mass of ith particle
ri = distance of ith particle from axis of rotation
Moment of inertia of triangle= Itri=61Mr2 --equation( 1 )
Complete step by step solution:
An overhead view of the cube is given below. When calculated using Pythagoras Theorem , the diagonal of a cube of edge length a turns out to be 2a . The distance between axis of rotation and a corner of the cube will be designated as r=22a=2a --equation( 2)
As per the figure given below, the moment of inertia of a face of the square plate face will be twice that of the triangle.
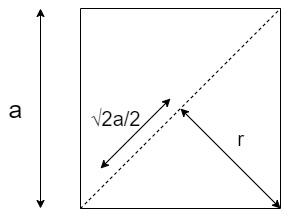
∴I=2×(moment of inertia of triangle)--equation( 3)
From equation 1 , moment of inertia of triangle = 61Mr2
∴ moment of inertia of square plate = 612Mr2 = 612M(2a)2 = 24Ma2--equation(4)
Notice that M has been replaced by 2M . This is because the mass of the triangle is half that of square.
Put equation (4) in (3) .
∴I=2×24Ma2=12Ma2 --equation (5)
Equation (5) represents moment of inertia of square plate along the diagonal, to calculate the moment of inertia of the cube, integrate it keeping in mind that the cube is made up of square plates each of mass dm from height 0 to a .
∴ moment of inertia of cube for the diagonal passing through face is
⇒0∫IdI=∫0M12a2dm
⇒I=12Ma2
Moment of inertia of a cube for a diagonal going through a face is 12Ma2.
Note: Moment of inertia is different for each axis of rotation.
If the moment of inertia for one of the axes was given, we could have used the theorem of perpendicular axis or the theorem of parallel axis too.
In this case it was convenient to take the mass of the triangular portion as half that of square because of uniform density only.
