Question
Question: Find the moment of inertia of the circular disc of mass \( M \) and radius \( R \) cut as shown in f...
Find the moment of inertia of the circular disc of mass M and radius R cut as shown in figure below, about an axis through A and normal to the plane of the disc.
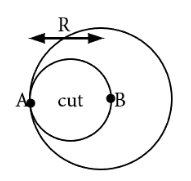
Solution
Hint : The total moment of inertia is the moment of inertia as though the hole hasn’t been there minus the moment of inertia if the hole had been a solid disk. The moment of inertia at an axis at the surface is equal to the moment of inertial at the centre plus the mass times the square of the radius of the disc.
Formula used: In this solution we will be using the following formula;
⇒Id=2MR2 , where Id , is the moment of inertia of a disc at an axis through its centre, M is the mass of the disc.
⇒Is=Ic+MR2 where Is is the moment of inertia about an axis at the surface , and Ic is the moment of inertia about an axis through its centre.
Complete step by step answer
To calculate the moment of inertia, we first assume that the hole is absent. The moment of inertia through A would be given by
⇒IA=IB+MR2 , where IA is the moment of inertia about an axis through A the surface , and IB is the moment of inertia about an axis through B, its centre, and M is the mass, R is the radius.
Hence,
⇒IA=2MR2+MR2=23MR2 (since Id=2MR2 , where Id , is the moment of inertia of a disc at an axis through its centre)
Now, we shall calculate the moment of inertia of the disk cutaway.
The disk has a radius of 2R
Mass can be given as M=σA=σ2πR2 where σ is surface density.
Hence, for the cut disk Mc=σA=σ2π(2R)2 .
⇒Mc=σ2π4R2=4M
Hence, Moment of inertia is given as
⇒IAC=21(4M(2R)2)+(4M(2R)2) , where IAC is the moment of inertia of the cutaway disk at an axis through A.
Hence,
⇒IAC=23[(4M4R2)]=323MR2
Now, since the disc with radius 2R is actually removed then, we subtract it from the moment of inertia of the whole disk.
Thus,
⇒IA−AC=23MR2−323MR2
Hence,
⇒IA−AC=23MR2(1−161)=23MR2×1615
⇒IA−AC=3245MR2.
Note
For clarity, the reason why we can simply subtract the moment of inertia is because the moment of inertia of any body is simply the rotational equivalent of mass. Just like the end mass of the cut disk would have been the mass of the whole disk minus the mass of the cut disk. The end moment of inertia is simply that but with mass replaced with moment of inertia.
