Question

Find the moment of inertia of a ring of mass $m$ and radius $R$ about an axis passing through its centre and making an angle of $45{}^\circ$ with its plane.

Answer 1

To solve this question, we need to have a knowledge about the parallel axis theorem. We will also have to use some other property because this will not be enough to solve this question. Using these two theorems we can find out the moment of inertia of the ring about an axis passing through its centre and making an angle of $45{}^\circ$ with its plane.

Complete answer:
By using parallel axis theorem, we can say that moment of inertia along the $x$ axis will be equal to the moment of inertia along the $y$ axis due to symmetry. Now, let us see the following diagram which makes this statement clearer. And let us assume that an axis $z$ passes perpendicularly to the plane formed by the $x$ axis and $y$ axis. This plane would pass along the diameter of the ring as such:

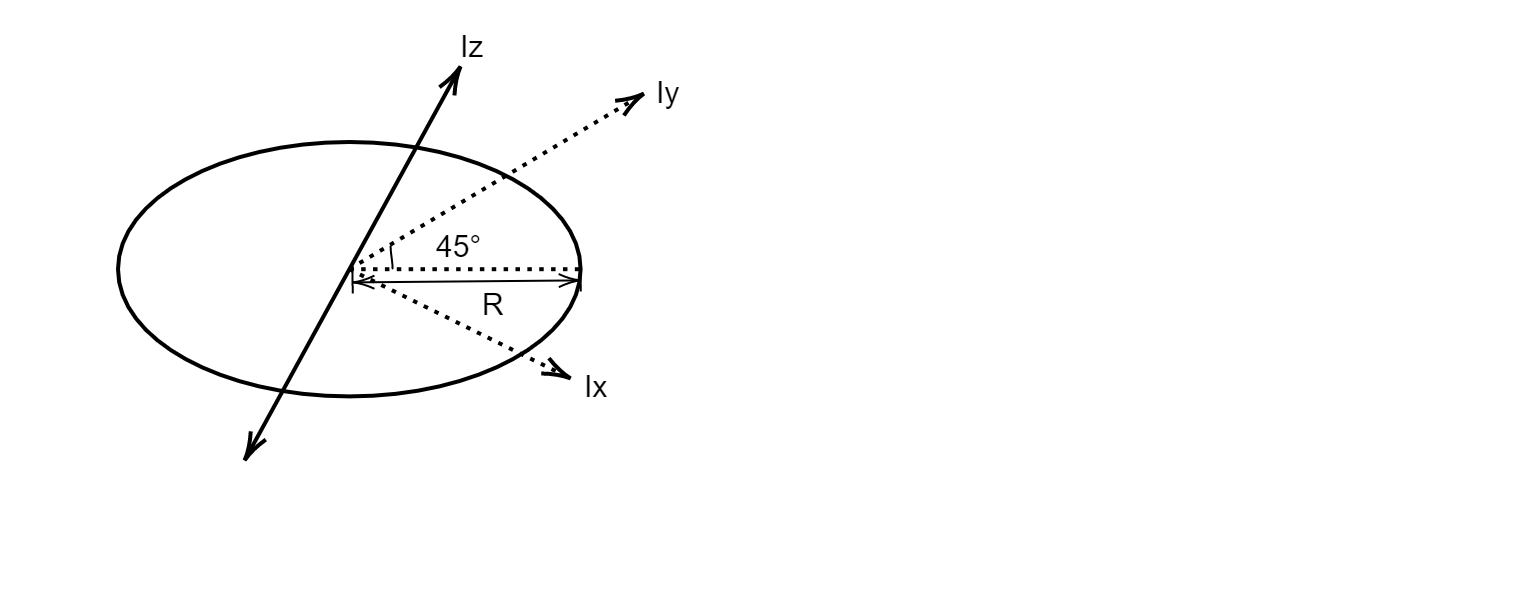
Now, we know that the moment of inertia of a ring about an axis passing through its diameter is:
${{I}_{z}}=\dfrac{m{{R}^{2}}}{2}$
We also know that:
${{I}_{x}}+{{I}_{y}}+{{I}_{z}}=2\sum{{{m}_{i}}r_{i}^{2}}$
Here ${{I}_{x}},{{I}_{y}},{{I}_{z}}$ are the moment of inertia about the three mutually perpendicular and intersecting axes,
${{m}_{i}}$ is the mass of the ${{i}^{th}}$ particle,
And ${{r}_{i}}$ is the distance from intersection
As we earlier said that ${{I}_{x}}={{I}_{y}}$, hence:
$\begin{aligned} & 2{{I}_{x}}+{{I}_{z}}=2m{{R}^{2}} \\\ & \Rightarrow 2{{I}_{x}}+\dfrac{m{{R}^{2}}}{2}=2m{{R}^{2}} \\\ & \Rightarrow 2{{I}_{x}}=2m{{R}^{2}}-\dfrac{m{{R}^{2}}}{2} \\\ & \Rightarrow 2{{I}_{x}}=\dfrac{4m{{R}^{2}}-m{{R}^{2}}}{2} \\\ & \Rightarrow 2{{I}_{x}}=\dfrac{3m{{R}^{2}}}{2} \\\ & \therefore {{I}_{x}}=\dfrac{3m{{R}^{2}}}{4} \\\ \end{aligned}$
Thus, the moment of inertia of ring of mass $m$ and radius $R$ about an axis passing through its centre and making an angle of $45{}^\circ$ with its plane is ${{I}_{x}}=\dfrac{3m{{R}^{2}}}{4}$.

Note:
According to the parallel axis theorem, the moment of inertia of a body about an axis is the sum of moment of inertia of the body about a parallel axis that passes through the center of mass of the body and the product of the mass of the body with the square of distance of the body from the parallel axis that passes through the center.