Question

Find the modulus, argument and the principal argument of the complex number $\dfrac{{2 + i}}{{4i + {{\left( {1 + i} \right)}^2}}}$.

Answer 1

Hint- Here, we will proceed by representing the given complex number in the form of any general complex number i.e., $z = x + iy$ and from there we will find the real and imaginary parts of the given complex number.

Complete step-by-step answer:
Let the given complex number be $z = \dfrac{{2 + i}}{{4i + {{\left( {1 + i} \right)}^2}}}{\text{ }} \to {\text{(1)}}$
As we know that the general form of any complex number is given by $z = x + iy{\text{ }} \to {\text{(2)}}$ where x is the real part of the complex number z and y is the imaginary part of the complex number z.
Now, we will convert the given complex number given by equation (1) in the same form as the general form of any complex number given by equation (2) as under
$\Rightarrow z = \dfrac{{2 + i}}{{4i + {1^2} + {i^2} + 2\left( 1 \right)\left( i \right)}}$
Using ${i^2} = - 1$ in the above equation, we get

$$\Rightarrow z = \dfrac{{2 + i}}{{4i + 1 + \left( { - 1} \right) + 2i}} \\\ \Rightarrow z = \dfrac{{2 + i}}{{6i}} \\\$$

In order to rationalize the above equation, we will multiply and divide the RHS of the above equation by i, we have
i.e.,

$$z = \dfrac{{i\left( {2 + i} \right)}}{{i\left( {6i} \right)}} \\\ \Rightarrow z = \dfrac{{2i + {i^2}}}{{6{i^2}}} \\\$$

Using ${i^2} = - 1$ in the above equation, we get

$$\Rightarrow z = \dfrac{{2i + \left( { - 1} \right)}}{{6\left( { - 1} \right)}} \\\ \Rightarrow z = - \left( {\dfrac{{2i - 1}}{6}} \right) \\\ \Rightarrow z = \dfrac{{1 - 2i}}{6} \\\ \Rightarrow z = \dfrac{1}{6} - \dfrac{{2i}}{6} \\\ \Rightarrow z = \dfrac{1}{6} - \dfrac{i}{3} \\\ \Rightarrow z = \dfrac{1}{6} + \left( {\dfrac{{ - 1}}{3}} \right)i{\text{ }} \to {\text{(3)}} \\\$$

By comparing equations (2) and (3), we get
Real part of the given complex part, $x = \dfrac{1}{6}$
Imaginary part of the given complex part, $y = \dfrac{{ - 1}}{3}$
As we know that the modulus of any complex number $z = x + iy$ is given by $\left| z \right| = \sqrt {{x^2} + {y^2}} {\text{ }} \to {\text{(4)}}$
Using the formula given by equation (4), we get
Modulus of the given complex number $z = \dfrac{{2 + i}}{{4i + {{\left( {1 + i} \right)}^2}}} = \dfrac{1}{6} + \left( {\dfrac{{ - 1}}{3}} \right)i{\text{ }}$ is given by
$\Rightarrow \left| z \right| = \sqrt {{{\left( {\dfrac{1}{6}} \right)}^2} + {{\left( {\dfrac{{ - 1}}{3}} \right)}^2}} \\\ \Rightarrow \left| z \right| = \sqrt {\dfrac{1}{{36}} + \dfrac{1}{9}} \\\ \Rightarrow \left| z \right| = \sqrt {\dfrac{{1 + 4}}{{36}}} = \sqrt {\dfrac{5}{{36}}} \\\ \Rightarrow \left| z \right| = \dfrac{{\sqrt 5 }}{6} \\\$
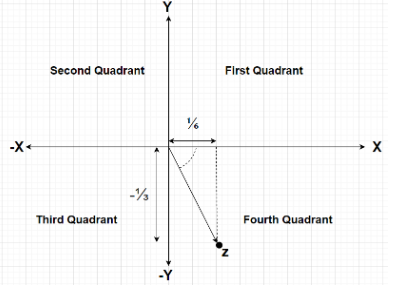
Since for the given complex number i.e., $z = \dfrac{{2 + i}}{{4i + {{\left( {1 + i} \right)}^2}}} = \dfrac{1}{6} + \left( {\dfrac{{ - 1}}{3}} \right)i$, the real part or x coordinate is positive and the imaginary part or y coordinate is negative. So, this complex number lies in the fourth quadrant.
Also, the principal argument (argument which lies between $- \pi$ to $\pi$) of any complex number $z = x + iy$ is given by Principal arg(z) = $ta{n^{ - 1}}\left( {\dfrac{y}{x}} \right)$ provided this value lies between $- \pi$ to $\pi$
Also, ${\tan ^{ - 1}}\left( { - \theta } \right) = - {\tan ^{ - 1}}\left( \theta \right)$
So, the principal argument of the given complex number $z = \dfrac{{2 + i}}{{4i + {{\left( {1 + i} \right)}^2}}} = \dfrac{1}{6} + \left( {\dfrac{{ - 1}}{3}} \right)i{\text{ }}$is given by
Principal arg(z) = $ta{n^{ - 1}}\left[ {\dfrac{{\left( {\dfrac{{ - 1}}{3}} \right)}}{{\left( {\dfrac{1}{6}} \right)}}} \right] = ta{n^{ - 1}}\left( { - 2} \right) = - ta{n^{ - 1}}\left( 2 \right) = - {63.44^0}$
In order to find the general argument for any complex number lying in the fourth quadrant, we will add $2n\pi$ to its principal argument.
Argument of the given complex number is arg(z) = $2n\pi$ + Principal arg(z)
Arg(z) = $2n\pi - {63.44^0}$.

Note- In this particular problem, we have found the modulus of the given complex number by using the formula $\left| z \right| = \sqrt {{x^2} + {y^2}}$ and the argument of the given complex number obtained by $ta{n^{ - 1}}\left( {\dfrac{y}{x}} \right)$ is clearly lying between $- \pi$ to $\pi$ or $- {180^0}$ to ${180^0}$ so it is the principal argument. The formula for the general argument of any complex number lying in the fourth quadrant is $2n\pi + ta{n^{ - 1}}\left( {\dfrac{y}{x}} \right)$.