Question

Find the modulus, argument and the principal argument of the complex number
${{\left( \tan 1-i \right)}^{2}}$. A.$\text{Modulus}={{\sec }^{2}}1,\arg \left( z \right)=2n\pi +\left( 2-\pi \right),\text{pricipal }\arg \left( z \right)=\left( 2-\pi \right)$
B. \text{Modulus}={{\operatorname{cosec}}^{2}}1,\arg \left( z \right)=2n\pi -\left( 2-\pi \right),\text{pricipal }\arg \left( z \right)=\left( -2-\pi \right)$$$$$ C. \text{Modulus}={{\sec }^{2}}1,\arg \left( z \right)=2n\pi -\left( 2-\pi \right),\text{pricipal }\arg \left( z \right)=-\left( 2-\pi \right) D. $\text{Modulus}=\text{cose}{{\text{c}}^{2}}1,\arg \left( z \right)=2n\pi +\left( 2-\pi \right),\text{pricipal }\arg \left( z \right)=\left( 2-\pi \right)

Answer 1

We express the given complex number ${{\left( \tan 1-i \right)}^{2}}$ in the form $z=a+ib$. We find its modulus using the formula $\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}$, the principal argument using the formula $\theta ={{\tan }^{-1}}\left( \dfrac{b}{a} \right),\theta \in \left( -\pi ,\pi \right]$ and all the arguments using the formula ${{\theta }_{n}}=\theta +2n\pi$ where $n\in Z.$$$$$

Complete step-by-step solution:
We know that the general form of a complex number is $z=a+ib$ where $a\in R$ is called the real part of $z$ and $b\in R$ is called the imaginary part of the complex number. The modulus of the complex number $z$ is given by
$\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}$

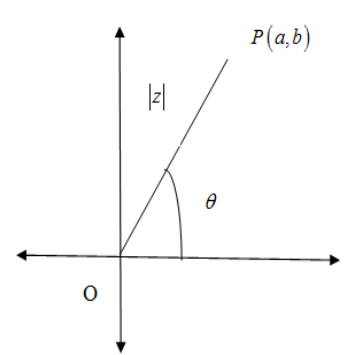
The modulus of the complex number represents the distance of the point $P\left( a,b \right)$ from the origin O in the complex plane. The principal argument of a complex number is a function which returns the measured counter-clockwise of the angle made by OP with positive real axis in radian . The principal argument $\theta$ which lies in the interval $\left( -\pi ,\pi \right]$ of the complex number is $z$ is
$\theta ={{\tan }^{-1}}\left( \dfrac{b}{a} \right),\theta \in \left( -\pi ,\pi \right]$
All other arguments of the complex number is $z$ with integer $n$ is
${{\theta }_{n}}=\theta +2n\pi$
We know the trigonometric identity involving the secant and tangent of the angle $A$ as,
${{\sec }^{2}}A-{{\tan }^{2}}A=1$
We are given in the question the complex number ${{\left( \tan 1-i \right)}^{2}}$. Let us express it in the form $z=a+ib$. So we have,

& z={{\left( \tan 1-i \right)}^{2}} \\\ & ={{\tan }^{2}}1+{{\left( i \right)}^{2}}-2i\tan 1 \\\ & ={{\tan }^{2}}1-1+i\left( -2\tan 1 \right) \\\ \end{aligned}$$ So we have obtained $a={{\tan }^{2}}-1,b=-2\tan 1$. So the modulus of $z={{\left( \tan 1-i \right)}^{2}}$ is,$$\begin{aligned} & \left| z \right|=\sqrt{{{\left( {{\tan }^{2}}1-1 \right)}^{2}}+{{\left( -2\tan 1 \right)}^{2}}} \\\ & =\sqrt{{{\tan }^{4}}1+1-2{{\tan }^{2}}1+4{{\tan }^{2}}1} \\\ & =\sqrt{{{\tan }^{4}}1+1+2{{\tan }^{2}}1} \\\ & =\sqrt{{{\left( {{\tan }^{2}}1+1 \right)}^{2}}} \\\ \end{aligned}$$ We use the relation between the secant and tangent of the angle for $A=1$ and have, $$\left| z \right|=\sqrt{{{\left( {{\sec }^{2}}1 \right)}^{2}}}={{\sec }^{2}}1$$ The principal argument of the complex number $z={{\left( \tan 1-i \right)}^{2}}$is $$\theta ={{\tan }^{-1}}\left( \dfrac{b}{a} \right)={{\tan }^{-1}}\left( \dfrac{-2\tan 1}{{{\tan }^{2}}-1} \right)={{\tan }^{-1}} \left( \dfrac{2\tan \left( 1 \right)}{1-{{\tan }^{2}}\left( 1 \right)} \right)$$ We have the formula for double angle of tangent $\tan 2A=\dfrac{2\tan A}{1-{{\tan }^{2}}A}$. So we get for $A=1$, $$\begin{aligned} & \theta ={{\tan }^{-1}}\left( \tan \left( 2\left( 1 \right) \right) \right) \\\ & ={{\tan }^{-1}}\left( \tan 2 \right) \\\ \end{aligned}$$ The solutions for above $\theta $ are $\theta =2+n\pi ,n\in Z$ but the principal argument lies in the interval $\left( -\pi ,\pi \right]$.So the integers satisfying principal is $n=-1,0$ and hence principal values are $\theta =2-\pi ,2$ out of which $\theta =2-\pi $ is in the options. We now find the other all other arguments of the complex number is $z$ with integer $n$ as $${{\theta }_{n}}=2n\pi +\left( 2-\pi \right)$$ **So we have $\text{Modulus}={{\sec }^{2}}1,\arg \left( z \right)=2n\pi +\left( 2-\pi \right),\text{pricipal }\arg \left( z \right)=\left( 2-\pi \right)$ and the correct option is A.** **Note:** We can also find the argument by converting the complex number $z=\tan 1-i$ to the form $z=r{{e}^{i\theta }}$ and then using the formula ${{z}^{2}}=\left| z \right|{{e}^{i\left( 2\theta \right)}}$ where $r$ is the modulus and $\theta $ is the principal argument. We have rejected negative values because modulus is always positive.