Question

Find the modulus and argument of the complex number $-\sqrt{3}+i$. $$$$

Answer 1

We recall the general form of a complex number $z=a+ib$, the modulus of the complex number $\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}$ and the argument of the complex number $\theta ={{\tan }^{-1}}\left( \dfrac{b}{a} \right)$. We compare the given complex number with the general form and find $a,b$ to find the modulus and argument. $$$$

Complete step by step answer:
We know that the general form of a complex number is $z=a+ib$ where $a$ is a real number and is called the real part of $z$ and $b$is a real number and is called the imaginary part of the complex number. The symbol $i$ represents the square root of negative unity that is $i=\sqrt{-1}$. In the Argand’ plane or complex plane the $x-$axis is represented as real axis and $y-$axis is represented as imaginary axis. Then the coordinate $Z\left( a,b \right)$ is represented as the position of complex number $z=a+ib$.

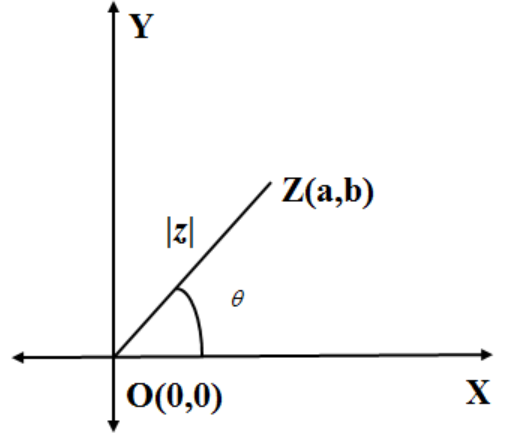
The modulus of a complex number is the distance between the complex number $Z\left( a,b \right)$ from the origin $O\left( 0,0 \right)$ and it is given by
$\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}$
The argument of the complex number is the measure of angle $OZ$ makes with the positive real axis and it is given by;
$\theta ={{\tan }^{-1}}\left( \dfrac{b}{a} \right)$
We are asked in the question to find the modulus and argument of the complex number$-\sqrt{3}+i$. We express it in the form of $z=a+ib=-\sqrt{3}+i=-\sqrt{3}+i\cdot 1$ and find that $a=-\sqrt{3},b=1$. So the modulus of complex number $-\sqrt{3}+i$ is
$z=\sqrt{{{a}^{2}}+{{b}^{2}}}=\sqrt{{{\left( -\sqrt{3} \right)}^{2}}+{{1}^{2}}}=\sqrt{3+1}=\sqrt{4}=2$
The argument of the complex number $-\sqrt{3}+i$ is,
$\theta ={{\tan }^{-1}}\left( \dfrac{b}{a} \right)={{\tan }^{-1}}\left( \dfrac{1}{-\sqrt{3}} \right)=\pi -{{\tan }^{-1}}\left( \dfrac{1}{\sqrt{3}} \right)=\pi -\dfrac{\pi }{6}=\dfrac{5\pi }{6}$

Note: We note that modulus is always a positive quantity since distance is always positive quantity and that is why we have rejected the negative square root. The argument $\theta ={{\tan }^{-1}}\left( \dfrac{b}{a} \right)$ is also called principal argument since tangent function is periodic and all other arguments are given by $n\pi +\theta$ where $n$ is any integer. The modulus is also denoted as $\bmod \left( z \right)$ and argument is also denoted as $\arg \left( z \right)$. If $\bmod \left( z \right)=r,\arg \left( z \right)=\theta$ then we can represent complex numbers $z=r{{e}^{i\theta }}$.