Question

Find the modulus and amplitude of the given complex number : $\sqrt 3 - i$

Answer 1

For any complex number $z = x + iy$, Modulus is $|z| = \sqrt {{x^2} + {y^2}}$ and amplitude $\theta = 2n\pi + \arg (z)$

Complete step by step answer:

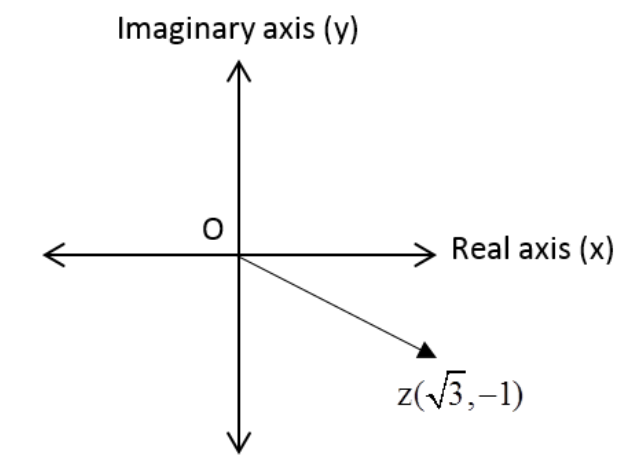
$\Rightarrow$ $z = \sqrt 3 - i$
From the diagram it can be seen that the point related to complex number z is in the fourth quadrant $(\sqrt 3 , - 1)$.
Comparing it with the standard equation, we get x = $\sqrt 3$ and y = -1.
Modulus $|z|$ is distance of point from origin.
$\Rightarrow$ $|z| = \sqrt {{{(\sqrt 3 )}^2} + {{( - 1)}^2}}$
$\Rightarrow$ $= \sqrt {3 + 1} = \sqrt 4 = 2$
$\Rightarrow$ $\arg (z) = - {\tan ^{ - 1}}\left| {\dfrac{y}{x}} \right|$ [As point is in IV quadrant]
$\Rightarrow$ $- {\tan ^{ - 1}}\left| {\dfrac{{ - 1}}{{\sqrt 3 }}} \right|$
$\Rightarrow$ $\dfrac{{ - \pi }}{6}$
Amplitude $= 2n\pi - \dfrac{\pi }{6}$

Note: General mistake done in calculating argument in fourth quadrant.
Sometimes we mistakenly take $(2\pi - \alpha )$ in place of $- \alpha$