Question

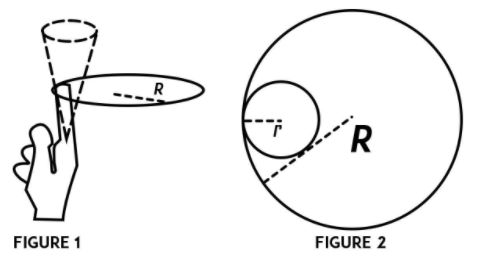
Find the minimum value of the angular velocity ${\omega _0}$ below which the ring that is being rotated drops down. (Figure 1 represents the rotation of the ring on the finger. The finger traces out a cone and Figure 2 represents the radii of the circular path that is traced out and the ring).

A) $\sqrt {\dfrac{{3g}}{{\mu \left( {R - r} \right)}}}$
B) $\sqrt {\dfrac{g}{{\mu \left( {R - r} \right)}}}$
C) $\sqrt {\dfrac{{2g}}{{2\mu \left( {R - r} \right)}}}$
D) $\sqrt {\dfrac{g}{{2\mu \left( {R - r} \right)}}}$

Answer 1

The normal force acting between the ring and the finger is directed inwards. It is the centripetal force. Here, ${\omega _0}$ is the angular velocity corresponding to the centripetal force of the ring to maintain its rotation on the finger. As the ring rotates, the frictional force comes into play. The force acting on the ring must overcome the friction to keep rotating.

Formulas used:
-The frictional force acting on a moving object must be such that $F \leqslant \mu N$ where $\mu$ is the coefficient of friction and $N$ is the normal force acting on the object.
-The centripetal force is given by, ${F_c} = m{\omega ^2}r$ where $m$ is the mass of the body, $\omega$ is its angular velocity and $r$ is the radius of the circular path along which the body rotates.

Complete step by step answer.
Step 1: Sketch a figure describing the different forces acting on the rotating ring and list the different parameters of the ring.

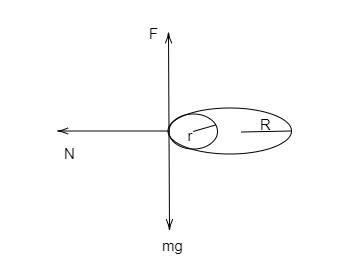
In the above figure, The frictional force acting between the finger and ring is denoted by $F$ and the weight of the ring $mg$ is directed downwards. The normal force is directed inwards to the centre of the circle along which the centre of mass of the ring moves.
A ring of mass $m$ and radius $R$ twirls near the tip of the finger. As the ring rotates, the finger traces out a cone as shown in figure 1. The radius $r$ is the radius of the circle traced out by the point of contact between the ring and the finger.
Let $\mu$ be the coefficient of friction that exists between the finger and the ring and $g$ be the acceleration due to gravity.
Step 2: Express the frictional force acting between the finger and the ring.
The frictional force acting on the point of contact between the ring and the finger is given by, $F \leqslant \mu N$ --------- (1)
where $\mu$ is the coefficient of friction and $N$ is the normal force acting on the ring.
Here the normal force constitutes the centripetal force acting on the ring.
The centre of mass of the ring moves with angular velocity ${\omega _0}$ along a circle.
From our rough figure, the radius of this circle will be $R - r$
Thus, the normal force can be expressed as $N = m\omega _0^2\left( {R - r} \right)$
The frictional force is balanced by the weight of the ring. $\therefore F = mg$
Substituting for $N = m\omega _0^2\left( {R - r} \right)$ and $F = mg$ in equation (1) we get, $mg \leqslant \mu m\omega _0^2\left( {R - r} \right)$
Cancel out $m$ on both sides and rearrange the equation to get, $\omega _0^2 \leqslant \dfrac{g}{{\mu \left( {R - r} \right)}}$
Taking the square root we get, ${\omega _0} \leqslant \sqrt {\dfrac{g}{{\mu \left( {R - r} \right)}}}$
Therefore, the minimum value of the angular velocity must be ${\omega _0} = \sqrt {\dfrac{g}{{\mu \left( {R - r} \right)}}}$ for the ring to not drop.

Hence the correct option is B.

Note: The normal force acting on an object is not always directed upwards. Here, the normal force is the force that is exerted to keep the ring from losing contact with the finger. Since it is the centripetal force that keeps an object in its circular path the normal force is essentially the centripetal force of the ring as in circular motion.