Question

Find the median value from the given table by drawing the curve of the values.

Weight (In kgs.)	No. of students
Less than $38$	$0$
Less than $40$	$3$
Less than $42$	$5$
Less than $44$	$9$
Less than $46$	$14$
Less than $48$	$28$
Less than $50$	$32$
Less than $52$	$35$

Answer 1

We will plot a cumulative frequency curve for the given distribution also called an ogive and then find the median using the graph.

Complete step-by-step solution:
From the question we know the cumulative frequency of the distribution. Since the last cumulative frequency is $35$ the given sample has the weight of total $35$ students.
Now, we have to plot the graph with taking the upper limit of weight on X-axis and the respective cumulative frequency on the Y-axis to get the less than ogive.
The points to be plotted to make a less than ogive are on the graph are: $(38,0),(40,3),(42,5),(44,9),(46,14),(48,28),(50,32),(52,35)$

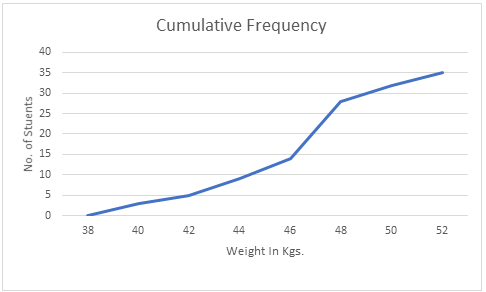
The Curve in the above graph is the Cumulative Frequency Curve i.e. the ogive.
Now to find the median:
Let $N$ be the total number of students whose data is given.
Also, $N$ will be the cumulative frequency of the last interval.
We find the ${\left[ {\dfrac{N}{2}} \right]^{th}}$ item and mark it on the y-axis.
In this case the ${\left[ {\dfrac{N}{2}} \right]^{th}}$ item is $(35/2)$ = $17.5$ student.
We draw a perpendicular from $17.5$ to the right to cut the Ogive curve.
From where the Ogive curve is cut, draw a perpendicular on the x-axis. The point at which it touches the x-axis will be the median value of the series as shown in the graph:

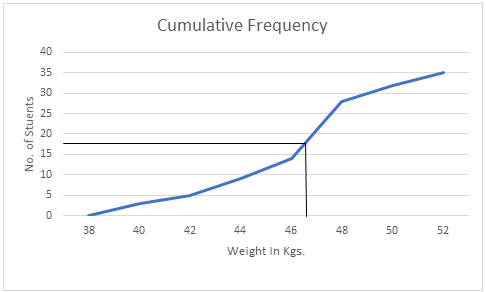
$\therefore$ From the above Graph we can see that the median is almost $47$ which is the required answer.

Note: The cumulative frequency should always be plotted on the Y-axis to get a correct ogive.
This was an example of a less than ogive, there also exists a more than ogive, in this type of ogive while making the cumulative frequency table, all the succeeding terms in the distribution should be added to a term in the table.