Question

Find the maximum value of the force to be applied so that the block in the figure does not move.

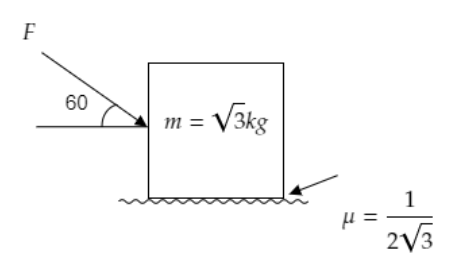
a. 20 N
b. 10 N
c. 12 N
d. 15 N

Answer 1

The block at rest experiences static friction and starts to move only when the applied force $F$ overcomes maximum static friction ${\left( {{f_s}} \right)_{\max }}$. Hence, the maximum value of force applied to not move the block must be equal to the maximum static friction for the block to remain stationary.

Complete step by step answer:
Step 1: Sketch the figure depicting the forces acting on the block with force $F$ resolved into its components. List the values of the known quantities.

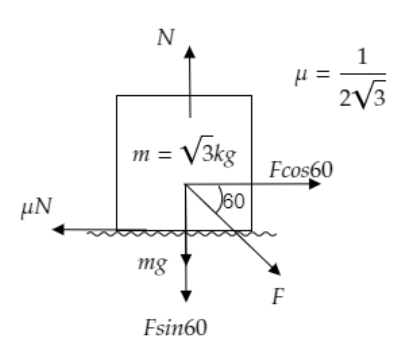
Given, the mass of the block is $m = \sqrt 3 {\text{kg}}$ and the coefficient of static viscosity is $\mu = \dfrac{1}{{2\sqrt 3 }}$ . The force $F$ acting on the block is directed at an angle $\theta = 60^\circ$ .

Step 2:
Obtain an expression for the forces acting vertically on the block of mass $m$ .
In the figure, the vertical component of the force, $F\sin 60^\circ$ and the weight of the block, $mg$ are in the same direction. Also, $F\sin 60^\circ$ and $mg$ appear to be antiparallel to the normal force $N$ .
Thus we can express the total forces acting on the block in the vertical direction by, $N = F\sin 60^\circ + mg$ ------(1).

Step 3:
Obtain an expression for the forces acting horizontally on the block of mass $m$ .
In the figure, the horizontal component of the force $F$ acting on the body is $F\cos 60^\circ$ .
Since the block is at rest, static friction ${f_s}$ acts on the block and is in a direction opposite to the horizontal component of the force which tries to move the block.
The limiting value of static friction is given by, ${\left( {{f_s}} \right)_{\max }} = \mu N$ , where $\mu$ is the coefficient of static friction and $N$ is the normal force acting on the block. This maximum static friction ${\left( {{f_s}} \right)_{\max }}$ is antiparallel to the horizontal component $F\cos 60^\circ$ .
Thus we can express the total forces acting on the block in the horizontal direction by, $F\cos 60^\circ = \mu N$ ------(2).

Step 4:
Obtain an expression for $F$ using equations (1) and (2).
Equation (1) gives us $N = F\sin 60^\circ + mg$ .
Equation (2) gives us $F\cos 60^\circ = \mu N$ .
Substitute (1) in (2) to get, $F\cos 60^\circ = \mu \left( {F\sin 60^\circ + mg} \right)$ .
On simplifying the above equation we get, $F\cos 60^\circ - \mu F\sin 60^\circ = \mu mg$ .
Substituting $\cos 60^\circ = \dfrac{1}{2}$ and $\sin 60^\circ = \dfrac{{\sqrt 3 }}{2}$ in the above equation to get, $\dfrac{1}{2}F - \mu \dfrac{{\sqrt 3 }}{2}F = \mu mg$ . Simplifying the above equation gives us, $\dfrac{F}{2}\left( {1 - \sqrt 3 \mu } \right) = \mu mg$ .
This then becomes, $F = \dfrac{{2\mu mg}}{{\left( {1 - \sqrt 3 \mu } \right)}}$ -----(3).
Substitute the values $m = \sqrt 3 {\text{kg, }}\mu = \dfrac{1}{{2\sqrt 3 }}$ and $g = 10{\text{m/}}{{\text{s}}^2}$ in equation (3) to get, $F = \dfrac{{2 \times \dfrac{1}{{2\sqrt 3 }} \times \sqrt 3 \times 10}}{{1 - \left( {\sqrt 3 \times \dfrac{1}{{2\sqrt 3 }}} \right)}} = 20{\text{N}}$ .
Therefore, the maximum force exerted on the given block so that it does not move is $F = 20{\text{N}}$ .

Hence, the correct answer is option (A).

Note: When a vector is resolved into its horizontal and vertical components the original vector makes an angle $\theta$ with its x component (horizontal component). Hence, the horizontal component of the vector is expressed in terms of $\cos \theta$ and the vertical component is expressed in terms of$\sin \theta$ as the vector along with its components constitutes a right triangle.