Question

Find the maximum speed at which a truck can safely travel without toppling over, on a curve of radius $250\;m$. The height of the center of gravity of the truck above the ground is $1.5\;m$ and the distance between the wheels is $1.5\;m$, the truck being horizontal.
A). $15\;ms^{-1}$
B). $25\;ms^{-1}$
C). $30\;ms^{-1}$
D). $35\;ms^{-1}$

Answer 1

For the truck to topple over, one of its wheels has to lose contact with the ground. This means that the normal reaction on one of the wheels will be zero, while the entire weight of the truck will be pivoted on the wheel. This, in turn, is balanced by the centripetal force that acts on the truck as friction between the wheel and the road.
When the truck is balanced, it does not topple over. So, equate the two moments associated with the forces mentioned before and this should lead you to an expression for the maximum velocity, to which you can substitute the values given in the question and arrive at the appropriate result.
Formula Used: Centripetal force $F_c = \dfrac{mv^2}{R}$

Complete step-by-step solution:
We are given that the truck travels through a circular path of radius $R = 250\;m$. Thus, if the truck exceeds a certain speed, chances are it topples over. Let this maximum speed be $v\;ms^{-1}$.
The diagram of the influencing forces looks as shown in the figure.
Let the center of gravity of the truck be at a height $h = 1.5\;m$ from the ground and let this be at a distance x from the outer wheel. Since the distance between the two wheels is $1.5\;m$, the center of gravity is at a distance of $\dfrac{1.5}{2} = 0.75\;m$ from either wheel. $\Rightarrow x =0.75\;m$
Let us consider the critical case where the truck is just about to topple. In this case, the normal reaction acting on the inner wheel $N_i$ will become zero since it will begin to lose contact with the road as it swerves. However, the normal reaction on the outer wheel assumes the entire gravitational force acting on the truck, i.e.,
$N = mg$.
In such a case, the frictional force provides the necessary centripetal force to pull the truck back into the curve. Therefore.
$F_{f} = F_{c} = \dfrac{mv^2}{R}$

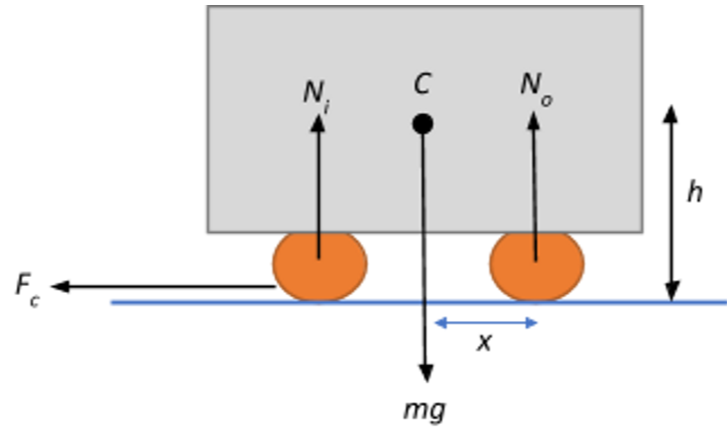
Now that we have defined the contributing forces, we can take the moments about the center of gravity C.
In doing so, for the truck to be balanced, we get:
$N_{o}(x) = F_{f}(h)$
$\Rightarrow mg(x) = \left(\dfrac{mv^2}{R}\right)h$
$\Rightarrow v^2 = \dfrac{gRx}{h} \Rightarrow v = \sqrt{\dfrac{gRx}{h}}$
$\Rightarrow v = \sqrt{\dfrac{9.8 \times 250 \times 0.75}{1.5}} = \sqrt{1225} = 35\;ms^{-1}$
Therefore, the correct choice would be $D. 35\;ms^{-1}$.

Note: We have extrapolated the principle of moments to understand vehicle dynamics in the problem given to us. The principle of moments states that the sum of clockwise moments will be equal to the sum of anticlockwise moments for a balanced system. In the problem, we have used the outer wheel to be the pivot about which we consider the clockwise and anticlockwise moments to just balance them out in order to prevent the truck from toppling over.