Question

Find the maximum magnifying power of a compound microscope having a $25\;$ diopter lens as the objective, a $5$ diopter lens as the eyepiece, and the separation $30\;cm$ between the two lenses. The least distance for clear vision is $25\;cm$.
(A) $8.4\;$
(B) $7.4\;$
(C) $9.4\;$
(D) $10.4\;$

Answer 1

A compound microscope consists of two lenses, the focal length of both lenses can be calculated by reciprocating their powers. It is known that the maximum magnification is achieved when the image is formed at the least distance of clear vision, thus all of these values can be then used to calculate the maximum magnifying power of the microscope.

Complete step by step solution:

The first step is to find the focal length of both the eyepiece and the objective lens.
We know that,
The focal length, $f$ of a lens, is given by-
$f = \dfrac{1}{P}$
where $P$ is the power of the lens.
Therefore, the focal length of the objective lens ${f_o}$is given by-
${f_0} = \dfrac{1}{{25}}m$
or in centimeters,
${f_o} = \dfrac{{100}}{{25}} = 4cm$
Similarly for the eyepiece,
The focal length ${f_e}$ is given by-
${f_e} = \dfrac{{100}}{5} = 20cm$
The light first enters the objective lens, then the image formed by the objective acts as an object for the eyepiece lens, and then the final image is formed by the eyepiece, which should be formed at $25cm\;$ for clear vision.
Therefore, the position of the image formed by the eyepiece ${v_e}$is-
${v_e} = - 25cm$
The lens formula is given by-
$\dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v}$
where $f$ is the focal length, $u$ is the position of the object, and $v$ is the position of the image formed.

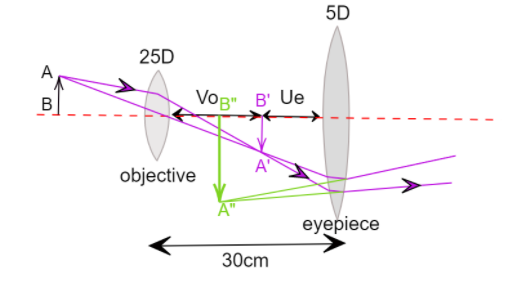
For the eyepiece lens, by applying the lens formula we see that-
$\dfrac{1}{{20}} = \dfrac{1}{{{u_e}}} + \dfrac{1}{{\left( { - 25} \right)}}$
$\Rightarrow \dfrac{1}{{20}} + \dfrac{1}{{25}} = \dfrac{1}{{{u_e}}}$
Upon rearranging,
$\dfrac{1}{{{u_e}}} = \dfrac{{4 + 5}}{{100}} = \dfrac{9}{{100}}$
$\Rightarrow {u_e} = \dfrac{{100}}{9} = 11.11cm$
We know that the distance between the lenses is $30cm\;$, and the position where the first image is formed lies between both lenses. The first image is made by the objective lens and acts as an object for the eyepiece lens, therefore the distance of this image $A'B'\;$ can be given by-${v_o} + {u_e} = 30$
${v_0} = 30 - 11.11$
$\Rightarrow {v_0} = 18.89cm$
The image is formed on the right of the objective lens and hence carries a positive sign with it.
Now applying the lens formula for the objective lens, we have-
$\dfrac{1}{{{f_o}}} = \dfrac{1}{{{u_o}}} + \dfrac{1}{{{v_o}}}$
Putting the values and rearranging,
$\dfrac{1}{{{u_o}}} = \dfrac{1}{4} - \dfrac{1}{{18.89}}$
$\Rightarrow \dfrac{1}{{{u_o}}} = 0.053 - 0.25 = - 0.197$
On reciprocating,
${u_o} = \dfrac{1}{{0.197}} = - 5.07cm$
$\Rightarrow {u_o} = - 5.07cm$
The maximum magnification power by a compound microscope is given by the formula-
$M = \dfrac{{{v_o}}}{{{u_o}}}\left( {1 + \dfrac{D}{{{f_e}}}} \right)$
$\Rightarrow M = \dfrac{{18.89}}{{( - 5.07)}}\left( {1 + \dfrac{{25}}{{20}}} \right)$
On simplifying,
$M = - 3.72 \times 2.25$
$\Rightarrow M = - 8.37$
The maximum magnification produced by the microscope is $8.37\;$and the image is inverted.

Since, $8.37 \approx 8.4$ the correct answer is option (A).

Note: It should be kept in mind that using the correct sign convention in each step is very important. A ray diagram is necessary in order to determine the sign convention of the position of an image or an object relative to a lens. Assuming that light travels from left to right, if the position of the object/image is on the left of the lens then it is negative and vice versa.