Solveeit Logo
Login

Question

Question: Find the maximum and minimum values of \({\sin ^{ - 1}}x + {\text{ta}}{{\text{n}}^{ - 1}}x.\)...

Find the maximum and minimum values of sin⁡−1x+tan−1x.{\sin ^{ - 1}}x + {\text{ta}}{{\text{n}}^{ - 1}}x.

Explanation

Solution

Here in these types of problems, where we are asked to find the maximum or minimum value of the given function, we need to see whether the graph is increasing or decreasing. If it is fully increasing or decreasing for the domain. Then the maximum and minimum values of the function will be at the maximum and minimum values of the domain.

Complete step-by-step answer:
Here we are given to find the maximum and minimum values of the function which is sin⁡−1x+tan−1x.{\sin ^{ - 1}}x + {\text{ta}}{{\text{n}}^{ - 1}}x.
We must know that the domain of sin⁡−1x=[−1,1]{\sin ^{ - 1}}x = \left[ { - 1,1} \right] and of tan−1x=(−∞,∞){\text{ta}}{{\text{n}}^{ - 1}}x = \left( { - \infty ,\infty } \right)
So if we need to find the common domain which means that the values that can be taken for the variable xx for both sin⁡−1x and tan−1x{\sin ^{ - 1}}x{\text{ and ta}}{{\text{n}}^{ - 1}}x at the same time. So the common domain will be [−1,1]\left[ { - 1,1} \right] because the value above 11 and below −1 - 1 will not satisfy the function sin⁡−1x{\sin ^{ - 1}}x
So for the common domain [−1,1]\left[ { - 1,1} \right] we need to find the maximum value of sin⁡−1x+tan−1x.{\sin ^{ - 1}}x + {\text{ta}}{{\text{n}}^{ - 1}}x.
We need to plot their graph as by seeing the graphs of both the functions we can come to know if they are increasing/decreasing or neither strictly increasing nor strictly decreasing.
Graph of sin⁡−1x{\sin ^{ - 1}}x

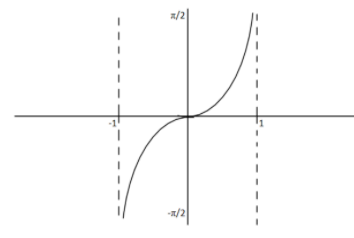
From the graph of sin⁡−1x{\sin ^{ - 1}}x we can notice that it is strictly increasing in its domain which is [−1,1]\left[ { - 1,1} \right]
Graph of tan−1x{\text{ta}}{{\text{n}}^{ - 1}}x

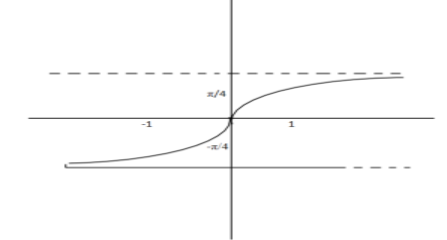
This graph also, as we notice, is strictly increasing for all the values that come in its domain.
Hence we can say that the function sin⁡−1x+tan−1x{\sin ^{ - 1}}x + {\text{ta}}{{\text{n}}^{ - 1}}x is strictly an increasing function.
Whenever the function is strictly increasing in the domain then we must know that the minimum and maximum values of the domain gives us the minimum and maximum values of the function.
Hence minimum value occurs at x=−1x = - 1
Minimum value of sin⁡−1x+tan−1x{\sin ^{ - 1}}x + {\text{ta}}{{\text{n}}^{ - 1}}x =sin⁡−1(−1)+tan−1(−1) = {\sin ^{ - 1}}\left( { - 1} \right) + {\text{ta}}{{\text{n}}^{ - 1}}\left( { - 1} \right)
Minimum value=−π2−π4=−2π−π4=−3π4 = - \dfrac{\pi }{2} - \dfrac{\pi }{4} = \dfrac{{ - 2\pi - \pi }}{4} = - \dfrac{{3\pi }}{4}
Maximum value will occur at x=1x = 1
Maximum value of sin⁡−1x+tan−1x{\sin ^{ - 1}}x + {\text{ta}}{{\text{n}}^{ - 1}}x =sin⁡−1(1)+tan−1(1) = {\sin ^{ - 1}}\left( 1 \right) + {\text{ta}}{{\text{n}}^{ - 1}}\left( 1 \right)
Maximum value=π2+π4=2π+π4=3π4 = \dfrac{\pi }{2} + \dfrac{\pi }{4} = \dfrac{{2\pi + \pi }}{4} = \dfrac{{3\pi }}{4}
Hence we get that:
Minimum value=−3π4 = - \dfrac{{3\pi }}{4}
Maximum value=3π4 = \dfrac{{3\pi }}{4}

Note: Here in these types of problems students can also proceed by using the differentiation of the function and equate it to zero to find whether the function is increasing or not but it can take some time. So we must always try to plot the graph first as it makes the solution clearer.