Question
Question: Find the mass \(M\) of the hanging block as shown in the figure which will prevent the smaller block...
Find the mass M of the hanging block as shown in the figure which will prevent the smaller block from slipping over the triangular block. All the surfaces are frictionless and the strings and the pulleys are light.
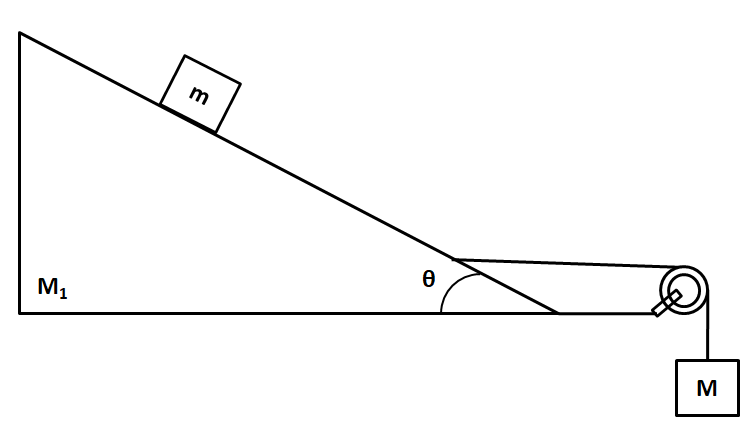
(A) (sinθ−1)m+M1
(B) (cosθ−1)m+M1
(C) (tanθ−1)m+M1
(D) (cotθ−1)m+M1
Solution
Hint
To solve this question, we have to draw the FBD for each of the blocks given in the question. Then, we have to use Newton's second law to obtain the equation of forces on the blocks. Solving those equations will lead us to the final answer.
Complete step by step answer
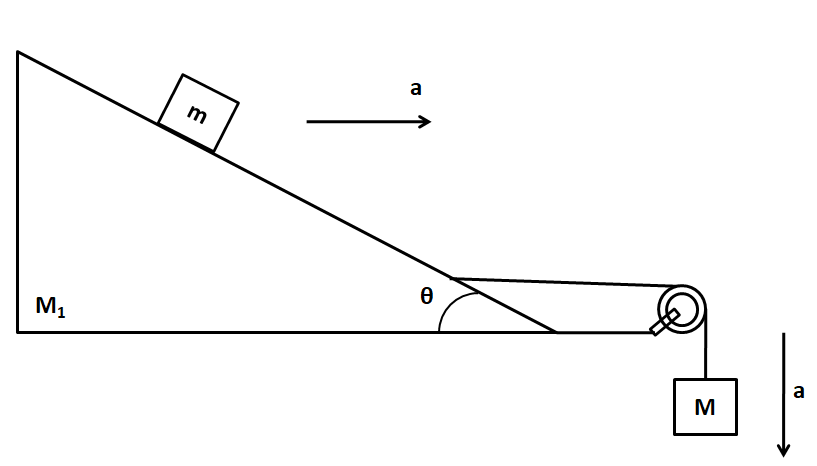
Let the acceleration of the hanging block of mass M be a downwards. Then, due to constraint motion, the acceleration of the triangular block of mass M1 will be a to the right.
Considering the FBD of the hanging block
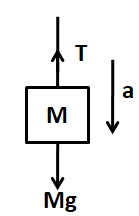
Mg−T=Ma (1)
Now, considering the FBD of the smaller block of massM
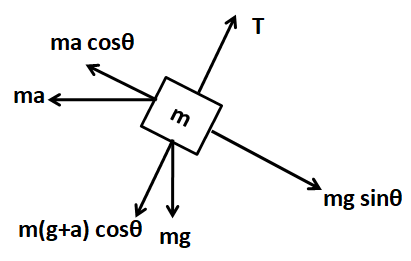
For no slipping, we have
⇒macosθ=mgsinθ
Dividing by mcosθ both the sides, we have
⇒a=gtanθ (2)
If the smaller block is not slipping over the triangular block, then the force of tension is pulling both the blocks as a single block of mass (M1+m) with the acceleration a.
∴T=(M1+m)a (3)
Substituting (3) in (1), we get
⇒Mg−(M1+m)a=Ma
⇒Mg−Ma=(M1+m)a
Taking M common
⇒M(g−a)=(M1+m)a
⇒M=(g−a)(M1+m)a (4)
Now substituting (2) in (4)
⇒M=(g−gtanθ)(M1+m)gtanθ
Dividing the numerator and the denominator by gtanθ we get
⇒M=(cotθ−1)(M1+m)
⇒M=(cotθ−1)m+M1
So, the mass of the hanging block which will prevent the smaller block from slipping is ⇒(cotθ−1)m+M1
Hence, the correct answer is option D.
Note
The force of tension cannot be directly transferred on to the smaller block. It is applied on the triangular block and the smaller block together as a system. The only force which can be applied on the smaller block is the pseudo force ma, which acts opposite to the acceleration of the triangular block, that is, towards the left.
