Question

Find the magnitude of the current supplied by the battery in the circuit shown in the figure. Also find the potential difference between the points P and Q.

Answer 1

Hint
To solve this question, first we need to determine the total current through the battery by finding the equivalent resistance in the circuit. Then using KCL and KVL we can determine the required value of the potential difference between the given points.

Formula Used: In this solution we will be using the following formula,
$\Rightarrow {R_{eq}} = {R_1} + {R_2} + {R_3} +. ...$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in series.
And $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} +. ...$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in a parallel circuit.

Complete step by step answer
Let the net current supplied by the battery be $I$
We begin by determining the net resistance of the circuit.
In the loop APBQ, the serial combination of the resistances ${R_1}$ and ${R_2}$ is connected in parallel to the serial combination of the resistances ${R_3}$ and ${R_4}$. So the resistance of the upper branch of the loop becomes
$\Rightarrow {R_u} = {R_1} + {R_2} = 6 + 6 = 12\Omega$
Also the resistance of the lower branch of the loop
$\Rightarrow {R_l} = {R_3} + {R_4} = 3 + 6 = 9\Omega$
Now these two resistances are in parallel combination. Hence the net resistance of the loop is given by
$\Rightarrow \dfrac{1}{{{R_N}}} = \dfrac{1}{{{R_u}}} + \dfrac{1}{{{R_l}}}$
$\Rightarrow \dfrac{1}{{{R_N}}} = \dfrac{1}{{12}} + \dfrac{1}{9}$
Taking the LCM as 36
$\Rightarrow \dfrac{1}{{{R_N}}} = \dfrac{{4 + 3}}{{36}}$
$\Rightarrow \dfrac{1}{{{R_N}}} = \dfrac{7}{{36}}$
Taking the reciprocal we get
$\Rightarrow {R_N} = \dfrac{{36}}{7}\Omega$
Now, as the internal resistance of the battery is connected in series with this loop,, the total resistance of the circuit becomes
$\Rightarrow R = {R_N} + r$
$\Rightarrow R = \dfrac{{36}}{7} + 1.5$
$\Rightarrow R = \dfrac{{36}}{7} + \dfrac{3}{2}$
Taking LCM as 14
$\Rightarrow R = \dfrac{{72 + 21}}{{14}}$
$\Rightarrow R = \dfrac{{93}}{{14}}\Omega$
Now the current supplied by the battery is given by
$\Rightarrow I = \dfrac{E}{R}$
According to the question, the voltage of the battery is
$\Rightarrow E = 6{\text{V}}$
So, we have
$\Rightarrow I = \dfrac{6}{{93}} \times 14$
$\Rightarrow I = \dfrac{{28}}{{31}}{\text{A}}$ … (1)
Now, let the current distribution in the branches of the loop be as shown below.

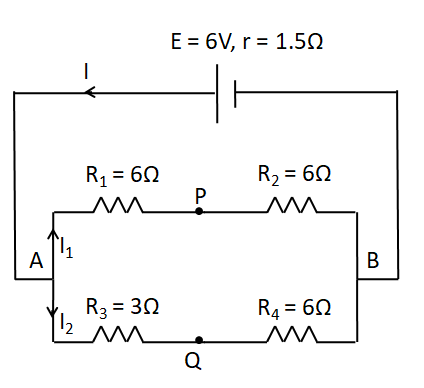
Applying KCL at A
$\Rightarrow I = {I_1} + {I_2}$
From (1)
$\Rightarrow {I_1} + {I_2} = \dfrac{{28}}{{31}}$ … (2)
Now, applying KVL in the loop APBQA
$\Rightarrow {I_1}{R_1} + {I_1}{R_2} - {I_2}{R_4} - {I_2}{R_3} = 0$
$\Rightarrow 6{I_1} + 6{I_1} - 6{I_2} - 3{I_2} = 0$
On simplifying we get
$\Rightarrow 12{I_1} - 9{I_2} = 0$
$\Rightarrow 12{I_1} = 9{I_2}$ … (3)
Solving (1) and (2) we get
$\Rightarrow {I_1} = \dfrac{{12}}{{31}}{\text{A}}$
$\Rightarrow {I_2} = \dfrac{{16}}{{31}}{\text{A}}$
Now, the potential difference between A and P is
$\Rightarrow {V_{AP}} = {I_1}{R_1}$
$\Rightarrow {V_{AP}} = \dfrac{{12}}{{31}} \times 6$
On solving we get
$\Rightarrow {V_{AP}} = \dfrac{{72}}{{31}}{\text{V}}$
Or, ${V_A} - {V_P} = \dfrac{{72}}{{31}}{\text{V}}$ (3)
Also the potential difference between A and Q is
$\Rightarrow {V_{AQ}} = {I_2}{R_3}$
$\Rightarrow {V_{AQ}} = \dfrac{{16}}{{31}} \times 3$
On solving
$\Rightarrow {V_{AQ}} = \dfrac{{48}}{{31}}{\text{V}}$
$\Rightarrow {V_A} - {V_Q} = \dfrac{{48}}{{31}}{\text{V}}$ … (4)
Subtracting (3) from (4) we have
$\Rightarrow \left( {{V_A} - {V_Q}} \right) - \left( {{V_A} - {V_P}} \right) = \dfrac{{48}}{{31}} - \dfrac{{72}}{{31}}$
$\Rightarrow {V_P} - {V_Q} = - \dfrac{{24}}{{31}}V$
Hence, the potential difference between the points P and Q is equal to $\dfrac{{24}}{{31}}{\text{V}}$.

Note
While calculating the net resistance of the circuit for calculating the net current supplied through the battery, we should not forget the internal resistance of the battery. Since it is not represented in the circuit by the conventional symbol of a resistance, we might forget to include it in our solution, and get the final answer wrong.