Question

Find the magnitude and direction of the magnetic induction vector $\overrightarrow{B}$ of an infinite plane carrying a current of linear density $\overrightarrow{i}$ ; the vector $\overrightarrow{i}$ is the same at all points of the plane.

Answer 1

You could use the right hand thumb rule to get the direction of magnetic induction. Now, you could consider an Amperian loop over the sheet and then apply Ampere’s circuital law to find the magnitude of magnetic induction. Note that, due to symmetrical distribution of current, the magnetic field perpendicular to the sheet gets canceled out.

Formula used: Ampere’s circuital law,
$\oint{B\centerdot dl={{\mu }_{0}}}I$

Complete step by step answer:
In the question, we are given an infinite plane carrying a current of linear charge density $\overrightarrow{i}$. If this current distribution is symmetric throughout the given plane, we are asked to find the magnitude and direction of the magnetic field induction vector $\overrightarrow{B}$ due to this infinite plane.

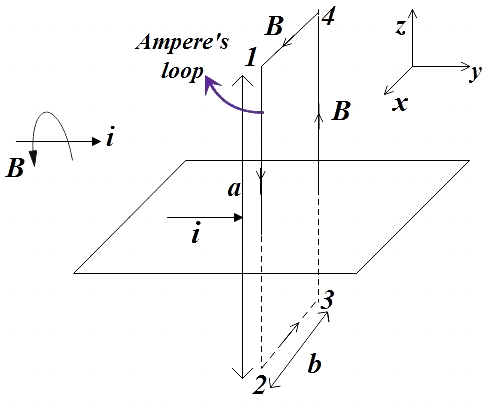
In the figure the current is directed along the positive y-axis, so we could find the direction of magnetic field using right hand thumb rule which states that if you point your right hand thumb in the direction of current then the curl of the rest of the fingers of your right hand gives the direction of the resultant magnetic field. Thereby, we get the direction of the magnetic induction $\overrightarrow{B}$ as shown in the figure.
Now, let us find the magnitude of the magnetic induction by using Ampere’s circuital law. This law states that the closed line integral of magnetic field around a current carrying conduction is absolute permeability ${{\mu }_{0}}$ times the total current passing through the surface. Mathematically,
$\oint{B\centerdot dl={{\mu }_{0}}}I$ ……………………….. (1)
Where, ‘$\overrightarrow{dl}$’ is a small line element on the Amperian loop considered.
We have considered a rectangular Amperian loop around the sheet as shown in the sheet, so, L.H.S of (1) can be given by,
$\oint{\overrightarrow{B}\centerdot \overrightarrow{dl}=}\int\limits_{1}^{2}{\overrightarrow{B\centerdot }\overrightarrow{da}}+\int\limits_{2}^{3}{\overrightarrow{B\centerdot }\overrightarrow{db}+\int\limits_{3}^{4}{\overrightarrow{B\centerdot }\overrightarrow{da}}}+\int\limits_{4}^{1}{\overrightarrow{B\centerdot }\overrightarrow{db}}$ …………………………….. (2)
Since the line elements on the loop is lying parallel to the direction of current, dot products can be given by,
$\overrightarrow{B}\centerdot \overrightarrow{da}=\left| \overrightarrow{B} \right|\left| \overrightarrow{da} \right|\cos 0=\left( B \right)\left( da \right)$
$\overrightarrow{B}\centerdot \overrightarrow{db}=\left| \overrightarrow{B} \right|\left| \overrightarrow{db} \right|\cos 0=\left( B \right)\left( db \right)$
Also,
$\int{\left( B \right)}\left( da \right)=B\int{da}=\left( B \right)\left( a \right)$
$\int{\left( B \right)}\left( db \right)=B\int{db}=\left( B \right)\left( b \right)$
Therefore,
$\Rightarrow \oint{\overrightarrow{B}}\centerdot \overrightarrow{dl}=\left( {{B}_{z}} \right)\left( a \right)+\left( {{B}_{x}} \right)\left( b \right)+\left( {{B}_{z}} \right)\left( a \right)+\left( {{B}_{x}} \right)\left( b \right)=2\left( {{B}_{z}} \right)\left( a \right)+2\left( {{B}_{x}} \right)\left( b \right)$ ………………………. (3)
Since we have a uniform distribution of current, the plane could be considered carrying an infinite number of filamentary current. Let us have a closer look at 2 such filamentary currents.

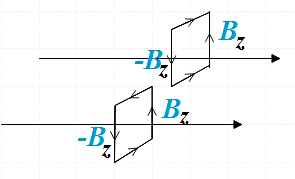
We see that for every ${{B}_{z}}$ there exists a$-{{B}_{z}}$, that lies very closely that they cancel out each other. So, all such components cancel out each other and along the z-direction we don’t have any magnetic field for the same reason.
Now, (3) becomes,
$\Rightarrow \oint{\overrightarrow{B}}\centerdot \overrightarrow{dl}=2\left( {{B}_{x}} \right)\left( b \right)$……………………. (4)
Now, for the R.H.S of (1) ‘$I$’ is the total current and we are given the current density. But we know current upon the perpendicular distance gives the current density, so,
$\overrightarrow{i}=\dfrac{I}{l}$
Where, ‘$I$’ is the total current and ‘$l$’is the perpendicular distance. Here,
$I=\overrightarrow{i}b$ ……………………… (5)
Substituting (4) and (5) in (1), we get,
$\Rightarrow 2Bb={{\mu }_{0}}\overrightarrow{i}b$
$\Rightarrow B=\dfrac{{{\mu }_{0}}\overrightarrow{i}}{2}$

Therefore, we get the magnetic induction of an infinite sheet as,
$B=\dfrac{{{\mu }_{0}}\overrightarrow{i}}{2}$
Where, ‘$\overrightarrow{i}$’ is the linear current density.

Note: We see that Ampere’s law for magnetic fields is analogous to Gauss law for electric fields. Both of them relate a physical quantity at the boundary (magnetic and electric fields) to the source in the interior (current and charge). Also, Ampere’s circuital law holds only for steady currents.