Question
Question: Find the magnetic field at point P due to a straight line segment \(AB\) of length \(6cm\) carrying ...
Find the magnetic field at point P due to a straight line segment AB of length 6cm carrying a current of 5A. (See figure)
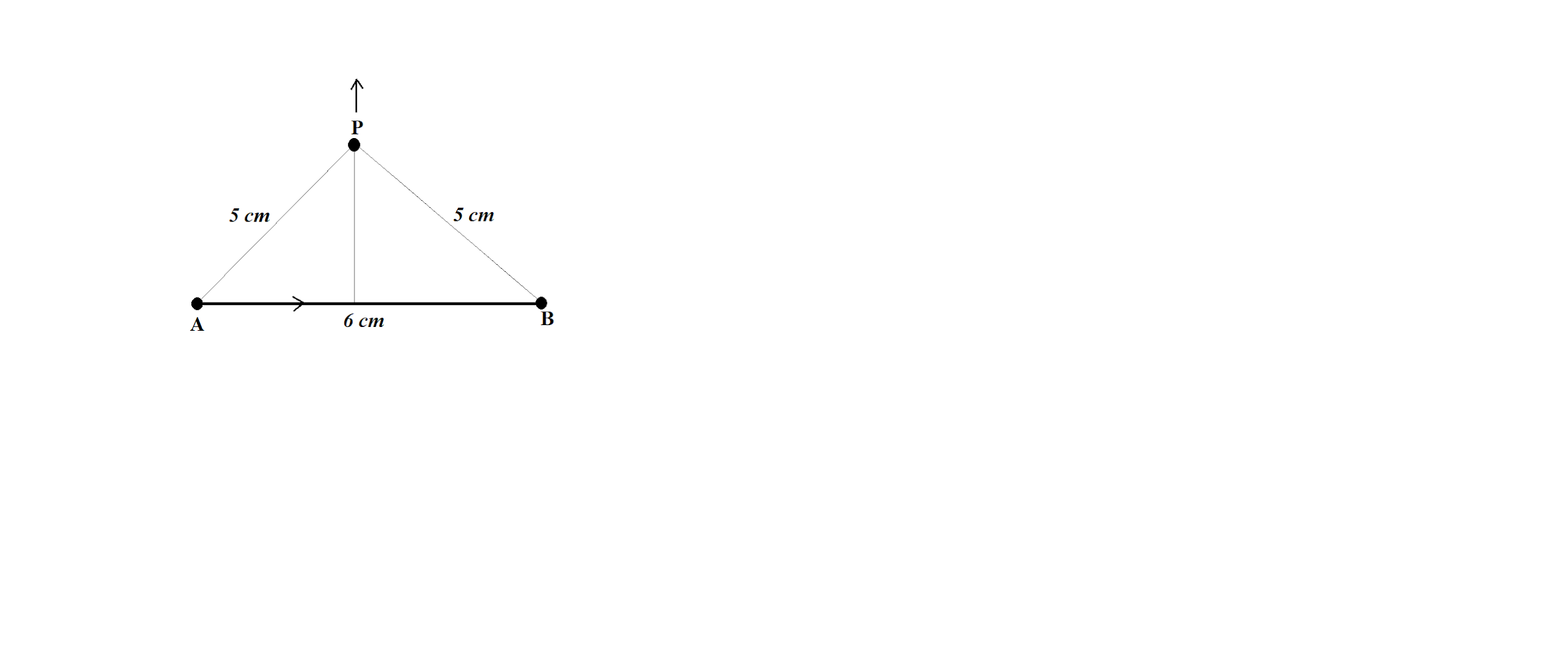
(μo=4π×10−7NA−2)
A. 3.0×10−5T
B. 2.5×10−5T
C. 2.0×10−5T
D. 1.5×10−5T
Solution
Hint: To find the value of magnetic field at point P, we will use the formula of magnetic field due to a straight current carrying wire segment at a point present on the equatorial axis of the segment.
Formula used:
B=4πrμoi(sinθ1+sinθ2)
Complete step by step answer:
Magnetic field is a vector field, or pseudo vector field, that describes the magnetic influence or impact of electric charges in relative motion with each other and effect of magnetized materials. A charge moving parallel to a current of other charges experiences a force perpendicular to its own velocity. We can say that the magnetic field is the area around a magnet in which there is presence of magnetic force. Magnetic field is a type of field that passes through space and which makes a magnetic force move electric charges and magnetic dipoles.
Suppose MN is a straight conductor carrying a current I and magnetic field intensity is to be determined at point X.
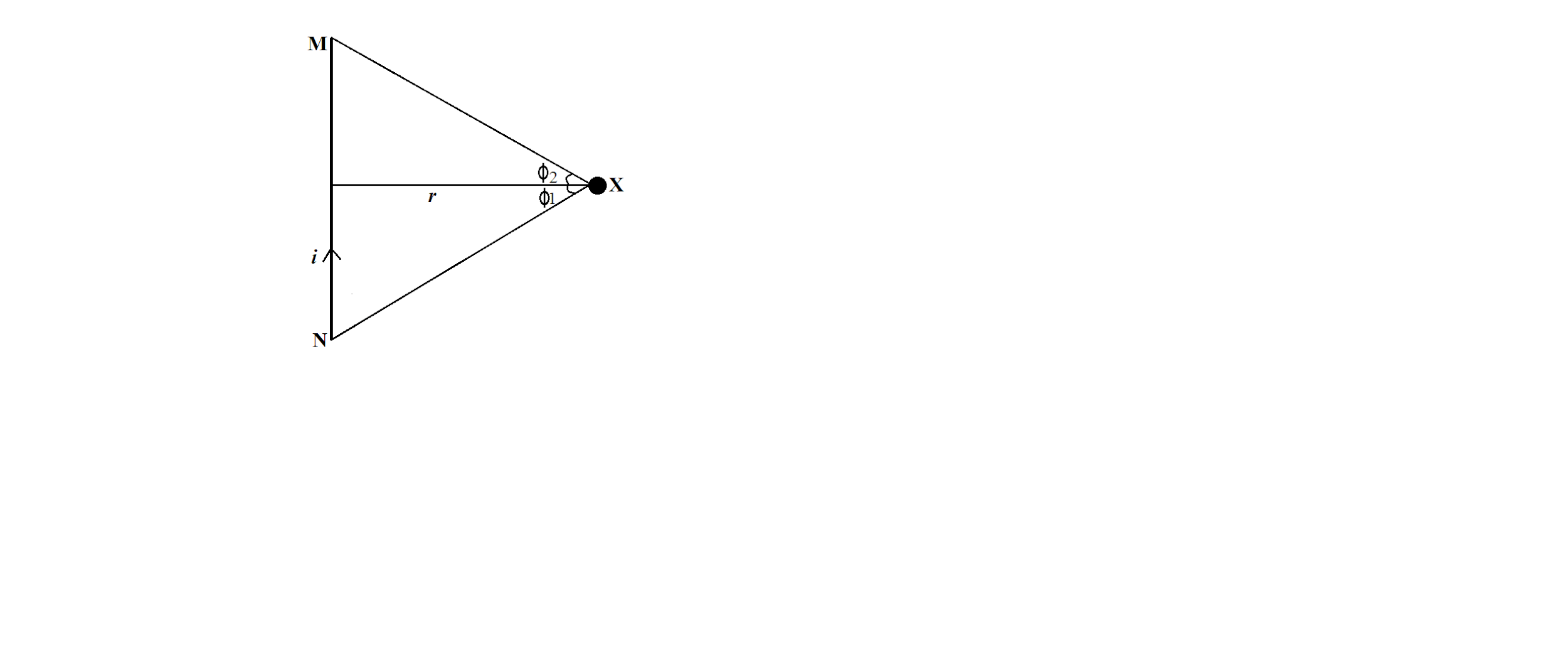
According to Biot-Savart law, magnetic field at point X is,
dB=4πμor3Idl×r
Angle between Idl and r is (180−θ), so,
dB=4πμor2Idlsin(180−θ)
dB=4πμor2Idlsinθ
Now, EG=EFsinθ=dlsinθ
And, EG=EPsindϕ=rsindϕ=rdϕ
We get, dlsinθ=rdϕ
Therefore, dB=4πμorIdϕ
Also, r=cosϕR
dB=4πμoRIcosϕdϕ
Total magnetic field at point X due to entire conductor is,
