Question

Find the magnetic field at P due to arrangement as shown.

Answer 1

In this question the bended wire arrangement can be considered as a system of two wires which are of semi-infinite length and aligned perpendicular to each other. So, the net magnetic field at Point ${{P}}$ can be found by superposition Principle i.e. by sum of magnetic fields due to two wires.

Formula used:
(i) ${{B}}\;{{ = }}\dfrac{{{{{\mu }}_{{0}}}}}{{{{4\pi }}}}\dfrac{{{I}}}{{{r}}}\left( {{{Sin}}{{{\theta }}_{{1}}}{{ - Sin}}{{{\theta }}_{{2}}}} \right)$
Where ${{B}}$ is magnetic field, ${{{\mu }}_{{0}}}$ is absolute permeability of free space, ${{I}}$ is amount of current flowing in the conductor, ${{r}}$ is perpendicular distance from the wire to the observation Point P, ${{{\theta }}_{{2}}}$ is the angle which the line joining Point P to lower end of wire makes with perpendicular line with the conductor/wire and ${{{\theta }}_{{1}}}$ is the angle which same perpendicular distance line makes with the line from point P to upper end of wire.

Complete step by step solution:
(i) Magnetic field due to wire $1$ As it is clear from the diagram the wire $1$ carries a current ${{I}}$ a point ${{P}}$ which is at ${{d}}$distance away from its lower end. And to point ${{P}}$ is given ${{PS}}\;{{ = }}\;{{dSin4}}{{{5}}^{{o}}}$
So,
{{PS}}\;{{ = }}\;\dfrac{{{d}}}{{\sqrt {{2}} }}{{\\_\\_\\_}}\left( {{1}} \right)
So, by right hand rule the direction of magnetic field at point ${{P}}$ due to wire $1$ is inward. If ${{B,}}$ in magnetic field at point ${{P}}$ due to wire $1$ end ${{PS}}$ is normal distance of wire from observation point then,
{{{B}}_{{1}}}\;{{ = }}\;\dfrac{{{{{\mu }}_{{0}}}}}{{{{4\pi }}}}\dfrac{{{I}}}{{{{PS}}}}\left( {{{Sin}}{{{\theta }}_{{1}}}{{ - Sin}}{{{\theta }}_{{2}}}} \right)\;{{\\_\\_\\_}}\left( {{2}} \right)
Also, from fig it is clear that ${{{\theta }}_{{1}}}{{ = }}\;{{9}}{{{0}}^{{o}}}{{,}}\;{{{\theta }}_{{2}}}{{ = }}\;{{4}}{{{5}}^{{o}}}$
By substituting the values of angles and ${{PS}}$ in equation $\left( 2 \right)$
We get
${{{B}}_{{1}}}{{ = }}\;\dfrac{{{{{\mu }}_{{0}}}}}{{{{4\pi }}}}\dfrac{{\sqrt {{2}} {{I}}}}{{{d}}}\left( {{{Sin9}}{{{0}}^{{o}}}{{ - Sin4}}{{{5}}^{{o}}}} \right)$
{{{B}}_{{1}}}\;{{ = }}\;\dfrac{{{{{\mu }}_{{0}}}}}{{{{4\pi }}}}\dfrac{{\sqrt {{2}} {{I}}}}{{{d}}}\left[ {{{1 - }}\dfrac{{{1}}}{{\sqrt {{2}} }}} \right]\;{{Inward}}\;{{\\_\\_\\_}}\left( 3 \right)

(ii) Magnetic field due to wire $2$ :
In the diagram ${{PQ}}$ is perpendicular distance of Point ${{P}}$ from:
Direction of current

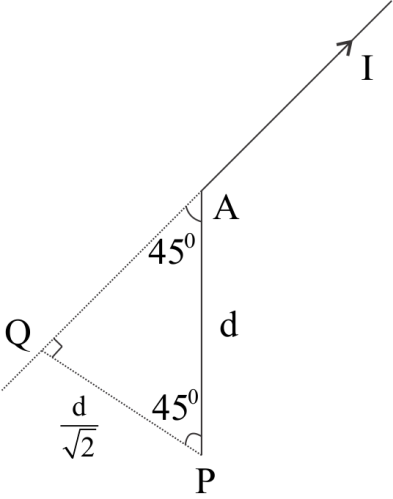
${{PQ}}\;{{ = }}\;{{dSin4}}{{{5}}^{{o}}}$
Here ${{{\theta }}_{{1}}}$ is ${90^ \circ }$ and
So, if ${{{B}}_{{2}}}$ is magnetic field at ${{P}}$ due to wire $2$ directing inwards by right hand rule is given by
{{{B}}_{{2}}}\;{{ = }}\dfrac{{{{{\mu }}_{{0}}}}}{{{{4\pi }}}}\dfrac{{{I}}}{{{{PQ}}}}\left( {{{Sin}}{{{\theta }}_{{1}}}{{ - Sin}}{{{\theta }}_{{2}}}} \right)\;{{\\_\\_\\_}}\left( {{5}} \right)

By substituting values of ${{PQ}}$ and ${{{\theta }}_{{1}}}{{,}}{{{\theta }}_{{2}}}$ in$\left( 5 \right)$ we get
${{{B}}_{{2}}}\;{{ = }}\dfrac{{{{{\mu }}_{{0}}}}}{{{{4\pi }}}}\dfrac{{\sqrt {{2}} {{I}}}}{{{d}}}\left( {{{Sin9}}{{{0}}^{{o}}}{{ - Sin4}}{{{5}}^{{o}}}} \right)$
{{{B}}_{{2}}}\;{{ = }}\;\dfrac{{{{{\mu }}_{{0}}}}}{{{{4\pi }}}}\dfrac{{\sqrt {{2}} {{I}}}}{{{d}}}\left( {{{1 - }}\dfrac{{{1}}}{{\sqrt {{2}} }}} \right)\;{{inwards}}\;{{\\_\\_\\_}}\left( {{6}} \right)
By equation $\left( 5 \right)$ and $\left( 6 \right),$ net magnetic field at ${{P}}$ is given by
${{B}}\;{{ = }}\;{{{B}}_{{1}}}{{ + }}{{{B}}_{{2}}}$
${{B}}\;{{ = }}\;\dfrac{{{{{\mu }}_{{0}}}}}{{{{4\pi }}}}{{.}}\dfrac{{\sqrt {{2}} {{I}}}}{{{d}}}\left( {{{1 - }}\dfrac{{{1}}}{{\sqrt {{2}} }}} \right){{ + }}\;\dfrac{{{{{\mu }}_{{0}}}}}{{{{4\pi }}}}\dfrac{{\sqrt {{2}} {{I}}}}{{{d}}}\left( {{{1 - }}\dfrac{{{1}}}{{\sqrt {{2}} }}} \right)$
${{B}}\;{{ = }}\;\dfrac{{{{{\mu }}_{{0}}}}}{{\sqrt {{2}} {{\pi }}}}\dfrac{{{I}}}{{{d}}}\left( {{{1 - }}\dfrac{{{1}}}{{\sqrt {{2}} }}} \right)$

Note: The distance ${{'r'}}$ which is used in the formula is perpendicular distance. So if it is not given then first find perpendicular distance by means of resolution of vectors and then substitute in the relation. The superposition principle is also known as superposition property. It states that, for all linear systems, the net response caused by two or more fields/forces is the sum of the responses that would have been caused by each stimulus individually.