Question

Find the lowest possible empirical formula in an arrangement of unit cells where A atoms are present at corners and alternate face centers, B atoms are present at alternate edge centres and C atoms are present at half of the mid of line joining opposite face centers. Assume: Any atom present in the inner locations of the unit cell should be considered completely within the unit cell structure.
(A) ${A_2}B{C_6}$
(B) ${A_2}{B_3}C$
(C) ${A_6}B{C_6}$
(D) ${A_6}{B_3}{C_3}$

Answer 1

Empirical formula of the chemical compound is defined as the simplest positive integer ratio of the atoms which are in the compound. The empirical formula does not mention the arrangement or number of atoms present in the molecules.

Complete answer:
To solve this question, we should know that an atom is shared by $8$ unit cell thus it gives $\dfrac{1}{8}th$ part of it. This is because there are $8$ corners in a unit cell. Thus, the total combination of A atoms present at corners
$\Rightarrow \dfrac{1}{8} \times 8 = 1$
These A atoms are also present at alternate face centers. Thus, A will be present at any two faces which would be opposite to each other. Contribution of the atom at the faces is $\dfrac{1}{2}$ . Thus, total contribution of A which is present at alternate faces
$\Rightarrow \dfrac{1}{2} \times 2 = 1$
Therefore, total number of A atoms is
$\Rightarrow 1 + 1 = 2$
Moving to B atom, it is present at an alternate edge center which can be four on which B is present. Thus, the total contribution of B
$\Rightarrow \dfrac{1}{4} \times 4 = 1$

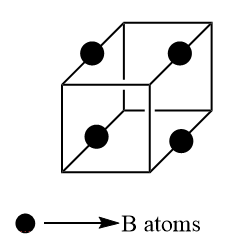
Unlike the other two, C atoms are present on the half of mid of the line which join the two face centers i.e. on the line, two atoms are present. There are $6$ faces thus $3$ lines joining the opposite face. There are two atoms in one line so the total number of the atoms is $6$ . Inside the unit, cell contribution is one. Thus, the total contribution of C atom is
$\Rightarrow 1 \times 6 = 6$

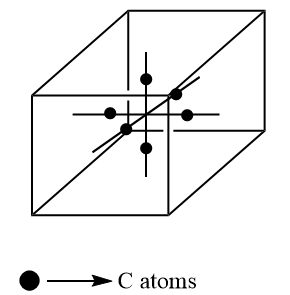
Thus, the empirical formula is ${A_2}B{C_6}$ that means option $\left( a \right)$ is correct.

Note:
The smallest representation of an entire crystal is a unit cell. All the crystal lattices are formed by the repetition of unit cells. In the unit cell, the coordination number of the atom is the number of atoms it is touching.