Question

Find the locus of the points of intersection of tangents drawn at the ends of all chords normal to the parabola ${{y}^{2}}=8\left( x-1 \right)$.

Answer 1

Hint: Assume $x-1=X$ and $y=Y$ and solve the whole question using the result of the standard parabola ${{y}^{2}}=4ax$. Later, replace $X$ and $Y$ with their actual values.

Complete step-by-step answer:

We are given a parabola ${{y}^{2}}=8\left( x-1 \right)$. We have to find the locus of the points of intersection of tangents drawn at the ends of the chords normal to the given parabola.

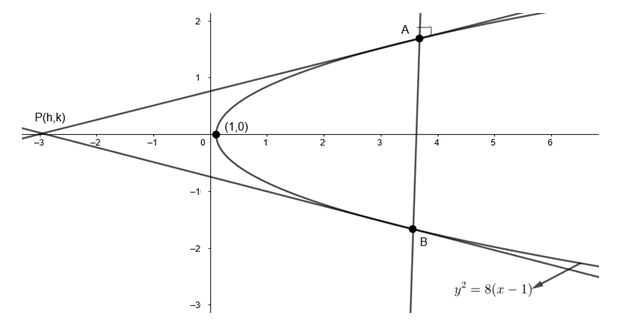
Let $P\left( h,k \right)$ be the point of intersection of tangents and $AB$ be the normal chord.

We are given parabola, ${{y}^{2}}=8\left( x-1 \right)$

Let$y=Y$ and $x-1=X$ to get a general parabola of the form ${{y}^{2}}=4ax$.

So now, we get a parabola ${{Y}^{2}}=8X$

Now, we know that for any parabola of the form ${{y}^{2}}=4ax$, equation of normal is
$y=mx-2am-a{{m}^{3}}$

For the given parabola, $4a=8$
So, we get $a=2$

So, our equation for normal to the parabola, ${{Y}^{2}}=8X$ which is $AB$ which is given by
$Y=mX-2am-a{{m}^{3}}$

Since, $a=2$, we get $Y=mX-4m-2{{m}^{3}}....\left( i \right)$

As $P\left( h,k \right)$ is the point of intersection of tangents at the ends of normal chord $AB$, therefore $AB$ would be a chord of contact with respect to a point $\left( h,k \right)$.

We know that equation of chord of contact of tangents drawn from a point $P\left( x,y \right)$ of the parabola ${{y}^{2}}=4ax$ is $y{{y}_{1}}=2a\left( x+{{x}_{1}} \right)$

Therefore, we get the equation of chord of contact of the point $\left( h,k \right)$ of the parabola ${{Y}^{2}}=8X$ is:
$Yk=2\times 2\left( X+h \right)$

Here, we get $Yk=4X+4h....\left( ii \right)$

Since we know that both equations $\left( i \right)$and $\left( ii \right)$ are the equation of chord $AB$.

Therefore, now we will compare the coefficients of $X$ and $Y$ and the constant of the equation $\left( i \right)$and $\left( ii \right)$.

Hence we get, $\dfrac{1}{k}=\dfrac{m}{4}=\dfrac{-\left( 4m+2{{m}^{3}} \right)}{4h}$

Taking $\dfrac{1}{k}=\dfrac{m}{4}$
We get, $m=\dfrac{4}{k}$

Taking $\dfrac{1}{k}=\dfrac{-\left( 4m+2{{m}^{3}} \right)}{4h}$
Now we will put the value of $m=\dfrac{4}{k}$.

Hence, we get $\dfrac{1}{k}=\dfrac{-\left( 4\left( \dfrac{4}{k} \right)+2{{\left( \dfrac{4}{k} \right)}^{3}} \right)}{4h}$

By cross multiplying above equation,
We get, $4h=-k\left[ \dfrac{16}{k}+\dfrac{128}{{{k}^{3}}} \right]$
$\Rightarrow 4h=-k\left[ \dfrac{16{{k}^{2}}+128}{{{k}^{3}}} \right]$

By cross multiplying above equation and canceling $4$ from both sides we get,
$h{{k}^{2}}=-4{{k}^{2}}-32$
Or, ${{k}^{2}}\left( h+4 \right)+32=0$

To find the locus, replace $h$ by $X$ and $k$ by $Y$
So, we get ${{Y}^{2}}\left( X+4 \right)+32=0$

As we had assumed that $Y=y$and $X=x-1$, therefore replacing $X$ and $Y$ with their actual values,
We get, ${{y}^{2}}\left( x-1+4 \right)+32=0$
${{y}^{2}}\left( x+3 \right)+32=0$

Therefore, the locus of points of intersection of tangents at the ends of the normal chord of the parabola ${{y}^{2}}=8\left( x-1 \right)$ is ${{y}^{2}}\left( x+3 \right)+32=0$

Note: Students must note that general equations of normals, tangents, etc are given for parabola for the form ${{y}^{2}}=4ax$ and for any variations in the general form of the parabola will also vary the equations of normals, tangents, etc. Always remember to replace $X$ and $Y$ with their actual values before assumption like in this question $X=x-1$ and $Y=y$