Question

Find the locus of the point of intersection perpendicular tangents to the circle ${x^2} + {y^2} = 10$.

Answer 1

Here, in the given question, we have been given an equation of circle and we are asked to find the locus of the point of intersection perpendicular tangent to the given circle. We will first find the centre of the circle and then the equation of the director circle to get the desired result.

Complete step-by-step solution:
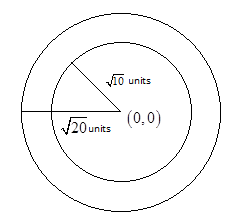
The equation of the given circle is ${x^2} + {y^2} = 10$.
We know that, ${x^2} + {y^2} = {r^2}$is the general equation of the circle having center at $\left( {0,0} \right)$and radius $r$units.
If we compare this general equation to the equation of a given circle, we get radius $r = \sqrt {10}$ units.
The director circle is the concentric circle whose radius is $\sqrt 2$times the radius of the given circle.
We know that the equation of the circle having Centre at origin and radius$r$units is${x^2} + {y^2} = {r^2}$.
So, the equation of the director circle with Centre at origin and radius $\sqrt {20}$units is

${x^2} + {y^2} = {\left( {\sqrt {20} } \right)^2}$
${x^2} + {y^2} = 20$
Hence, the equation of the director circle is${x^2} + {y^2} = 20$.
Thus, the locus of the point of intersection of perpendicular tangents to circle${x^2} + {y^2} = 10$is${x^2} + {y^2} = 20$.

Note: The locus of points of intersection of two perpendicular tangents to a circle is known as the director circle. The director circle is a concentric circle whose radius is$\sqrt 2$times the radius of the given circle. In short we can say that if circle is centred at origin then the equation of the point of intersection perpendicular tangents to circle${x^2} + {y^2} = {r^2}$will simply be written as${x^2} + {y^2} = 2{\left( r \right)^2}$.