Question

Find the locus of the point of intersection of perpendicular tangents to the circle $S \equiv {x^2} + {y^2} - 2x + 2y - 2 = 0$, that is, find the director circle of $S = 0$.

Answer 1

Hint: First of all, find the centre of the circle and radius of the given circle. Then find the equation of the director circle as the director circle is a concentric circle whose radius is $\sqrt 2$ times the radius of the given circle.
Complete step-by-step answer:
The equation of the circle is $S \equiv {x^2} + {y^2} - 2x + 2y - 2 = 0$.
We know that for the circle equation $S \equiv a{x^2} + b{y^2} + 2gx + 2fy + c = 0$, centre of the circle is $\left( { - g, - f} \right)$ and radius is $\sqrt {{g^2} + {f^2} - c}$.
If we compare the given circle equation i.e., $S \equiv {x^2} + {y^2} - 2x + 2y - 2 = 0$ with the standard circle equation $S \equiv a{x^2} + b{y^2} + 2gx + 2fy + c = 0$, we have $g = - 1$ and $f = 1$.
So, the centre of the given circle is $\left( {1, - 1} \right)$ and radius is$\sqrt {{{\left( { - 1} \right)}^2} + {{\left( 1 \right)}^2} - \left( { - 2} \right)} = \sqrt 4 = 2$.

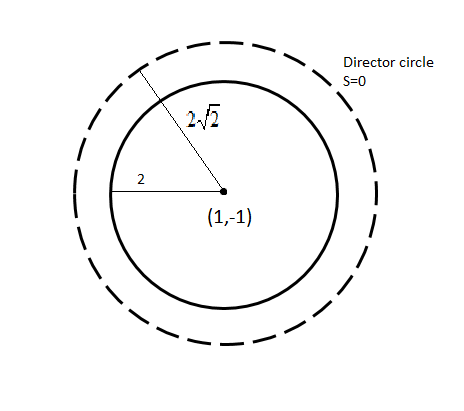
We know that the director circle is a concentric circle whose radius is $\sqrt 2$ times the radius of the given circle. And the equation of the circle with centre $\left( {h,k} \right)$ and radius $r$ is given by ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$.
So, the equation of the director circle with centre $\left( {1, - 1} \right)$ and radius $2\sqrt 2$ is given by

$$\Rightarrow {\left( {x - 1} \right)^2} + {\left( {y - \left( { - 1} \right)} \right)^2} = {\left( {2\sqrt 2 } \right)^2} \\\ \Rightarrow {x^2} - 2x + 1 + {\left( {y + 1} \right)^2} = {\left( 2 \right)^2}{\left( {\sqrt 2 } \right)^2} \\\ \Rightarrow {x^2} - 2x + 1 + {y^2} + 2y + 1 = 8 \\\ \Rightarrow {x^2} + {y^2} - 2x + 2y + 1 + 1 - 8 = 0 \\\ \therefore {x^2} + {y^2} - 2x + 2y - 6 = 0 \\\$$

Hence, the equation of the director circle is $S = {x^2} + {y^2} - 2x + 2y - 6 = 0$.
Thus, the locus of the point of intersection of perpendicular tangents to the circle $S \equiv {x^2} + {y^2} - 2x + 2y - 2 = 0$, that is, the director circle is $S = {x^2} + {y^2} - 2x + 2y - 6 = 0$.
Note: The locus of points of intersection of two perpendicular tangents to a circle is called the director circle. For the circle equation $S \equiv a{x^2} + b{y^2} + 2gx + 2fy + c = 0$, centre of the circle is $\left( { - g, - f} \right)$ and radius is $\sqrt {{g^2} + {f^2} - c}$.