Question

Find the locus of the midpoint of the chord of the parabola ${{y}^{2}}=4ax$, which passes through the point $\left( 3b,b \right)$.

Answer 1

Hint: Write the equation of chord and satisfy the given point and use formula for midpoint which is $x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2},y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$.

Complete step-by-step answer:
We are given a chord of the parabola which passes through the point $\left( 3b,b \right)$.
Here, we have to find the locus of midpoint of a given chord.

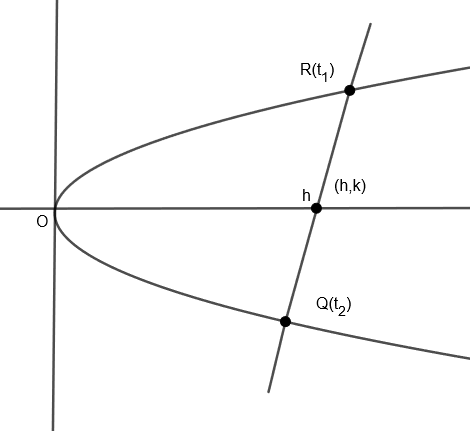
Let the midpoint of the given chord be $\left( h,k \right)$.
We know that any general point on parabola $P\left( t \right)$ is $\left( a{{t}^{2}},2at \right)$.
So, we get point $R\left( {{t}_{1}} \right)=\left( at_{1}^{2},2a{{t}_{1}} \right)$ and point $Q\left( {{t}_{2}} \right)=\left( at_{2}^{2},2a{{t}_{2}} \right)$
We know that equation of any line passing through $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is
$\left( y-{{y}_{1}} \right)=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}\left( x-{{x}_{1}} \right)$
Therefore, we get equation of chord passing through $R\left( {{t}_{1}} \right)=\left( at_{1}^{2},2a{{t}_{1}} \right)$ and point $Q\left( {{t}_{2}} \right)=\left( at_{2}^{2},2a{{t}_{2}} \right)$ as,
$\left( y-2a{{t}_{1}} \right)=\dfrac{\left( 2a{{t}_{2}}-2a{{t}_{1}} \right)}{\left( at_{2}^{2}-at_{1}^{2} \right)}\left( x-at_{1}^{2} \right)$
By cancelling the like terms, we get,
$\left( y-2a{{t}_{1}} \right)=\dfrac{2\left( {{t}_{2}}-{{t}_{1}} \right)}{\left( t_{2}^{2}-t_{1}^{2} \right)}\left( x-at_{1}^{2} \right)$
Since we know that,
$\left( {{a}^{2}}-{{b}^{2}} \right)=\left( a-b \right)\left( a+b \right)$
Therefore, we get,
$\left( y-2a{{t}_{1}} \right)=\dfrac{2\left( {{t}_{2}}-{{t}_{1}} \right)}{\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)}\left( x-at_{1}^{2} \right)$
By cancelling the like terms, we get,
$\left( y-2a{{t}_{1}} \right)=\dfrac{2\left( x-at_{1}^{2} \right)}{\left( {{t}_{2}}+{{t}_{1}} \right)}$
After cross multiplying the above equation, we get,
$\left( y-2a{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)=2\left( x-at_{1}^{2} \right)$
Simplifying the equation, we get,
$y\left( {{t}_{2}}+{{t}_{1}} \right)-2a{{t}_{1}}{{t}_{2}}-2at_{1}^{2}=2x-2at_{1}^{2}$
Finally, we get
$y\left( {{t}_{2}}+{{t}_{1}} \right)-2a{{t}_{1}}{{t}_{2}}=2x.....\left( i \right)$
Now, we know that midpoint say $\left( x,y \right)$ of any line joining points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$is:
$x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$ and $y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$
Therefore, we get the midpoint $\left( h,k \right)$ of chord joining $R\left( {{t}_{1}} \right)=\left( at_{1}^{2},2a{{t}_{1}} \right)$ and point $Q\left( {{t}_{2}} \right)=\left( at_{2}^{2},2a{{t}_{2}} \right)$ as:
$h=\dfrac{at_{1}^{2}+at_{2}^{2}}{2}....\left( ii \right)$
$k=\dfrac{2a{{t}_{1}}+2a{{t}_{2}}}{2}....\left( iii \right)$
Taking 2a common from equation $\left( iii \right)$, we get,
$k=\dfrac{2a\left( {{t}_{1}}+{{t}_{2}} \right)}{2}$.
Therefore, we get,
$\dfrac{k}{a}=\left( {{t}_{1}}+{{t}_{2}} \right)....\left( iv \right)$
Taking ‘a’ common from equation$\left( ii \right)$, we get,
$h=\dfrac{a\left( t_{1}^{2}+t_{2}^{2} \right)}{2}$
Or, $\dfrac{2h}{a}=t_{1}^{2}+t_{2}^{2}$
Since, we know that ${{a}^{2}}+{{b}^{2}}+2ab={{\left( a+b \right)}^{2}}$
Now, we subtract 2ab from both sides. We get,
${{a}^{2}}+{{b}^{2}}={{\left( a+b \right)}^{2}}-2ab$
Therefore, we get,
$\dfrac{2h}{a}={{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-2{{t}_{1}}{{t}_{2}}$
Now, we put the value of $\left( {{t}_{1}}+{{t}_{2}} \right)$ from equation (iv). We get,
$\dfrac{2h}{a}={{\left( \dfrac{k}{a} \right)}^{2}}-2{{t}_{1}}{{t}_{2}}$
Or $2{{t}_{1}}{{t}_{2}}=\dfrac{{{k}^{2}}}{{{a}^{2}}}-\dfrac{2h}{a}$
By dividing both sides by 2, we get,
${{t}_{1}}{{t}_{2}}=\dfrac{{{k}^{2}}}{2{{a}^{2}}}-\dfrac{h}{a}.....\left( v \right)$
Now, we will put the values of $\left( {{t}_{1}}+{{t}_{2}} \right)$ and $\left( {{t}_{1}}{{t}_{2}} \right)$ from equation $\left( iv \right)$and $\left( v \right)$ in equation $\left( i \right)$.
We get,
$y\left( {{t}_{2}}+{{t}_{1}} \right)-2a\left( {{t}_{1}}{{t}_{2}} \right)=2x$
$\Rightarrow y\left( \dfrac{k}{a} \right)-2a\left( \dfrac{{{k}^{2}}}{2{{a}^{2}}}-\dfrac{h}{a} \right)=2x$
$\Rightarrow \dfrac{yk}{a}-2a\left( \dfrac{{{k}^{2}}-2ha}{2{{a}^{2}}} \right)=2x$
By cancelling the like terms, we get,
$\Rightarrow \dfrac{yk}{a}-\dfrac{\left( {{k}^{2}}-2ha \right)}{a}=2x$
After simplifying and cross-multiplying above equation, we get,
$\left( yk \right)-\left( {{k}^{2}}-2ha \right)=2xa$
Now, we are given that this chord passes through point $\left( 3b,b \right)$.
Therefore, we will put $x=3b$ and $y=b$.
We get,
$bk-\left( {{k}^{2}}-2ha \right)=2\left( 3b \right)a$
$\Rightarrow bk-{{k}^{2}}+2ha=6ab$
By transposing all the terms to one side,
We get,
${{k}^{2}}-bk-2ha+6ab=0$
Now, to get the locus, we will replace h by x and k by y. We get,
${{y}^{2}}-by-2ax+6ab=0$
So, the locus of the midpoint of chord passing through $\left( 3b,b \right)$ is ${{y}^{2}}-by-2ax+6ab=0$.

Note: In these types of questions, we can directly write the equation of chord with respect to mid-point say $\left( {{x}_{1}},{{y}_{1}} \right)$ which is $\left( y-{{y}_{1}} \right)=\dfrac{2a}{{{y}_{1}}}\left( x-{{x}_{1}} \right)$ and put $\left( h,k \right)$ in place of $\left( {{x}_{1}},{{y}_{1}} \right)$ and point through which chord in passing [here (3b,b)] in place of $\left( x,y \right)$ to get locus of midpoint of chord.