Solveeit Logo
Login

Question

Question: Find the locus of midpoint of all chords of the circle \({{x}^{2}}+{{y}^{2}}-2x-2y=0\) such that pai...

Find the locus of midpoint of all chords of the circle x2+y2−2x−2y=0{{x}^{2}}+{{y}^{2}}-2x-2y=0 such that pair of lines joining (0, 0) and the point of intersection of the chords with the circles make equal angle with x axis.

Explanation

Solution

Let us assume the midpoint of the chord is (h, k). The using this point (h, k), write the equation of chord on the circle x2+y2−2x−2y=0{{x}^{2}}+{{y}^{2}}-2x-2y=0 by using the formula T=S1T={{S}_{1}} where S1{{S}_{1}} is the expression that we got after substituting the point (h, k) in the equation of circle x2+y2−2x−2y{{x}^{2}}+{{y}^{2}}-2x-2y and T is equal to: hx+ky−2(x+h2)−2(y+k2)hx+ky-2\left( \dfrac{x+h}{2} \right)-2\left( \dfrac{y+k}{2} \right) . Then homogenize this equation of circle using the equation of a chord by making each term in the equation of circle as degree 2. This homogenization will give you the multiplication of the equation of pairs of lines which are drawn from origin to the extremities of the chord. Now, this equation is a pair of lines so it has two lines or two slopes and then we are going to write the sum of the slopes. And as it is given that the pair of lines from origin are making an equal angle with the x axis it means that one of the slopes is positive and the other slope is negative and their magnitude are same because angle is equal with respect to x axis which will give us the sum of slopes as 0. Now, equating the sum of slopes as 0 will give you the relation between h and k then substitute h and k with x and y respectively to get the locus of the midpoint of the chords.

Complete step-by-step answer:
We have given a circle x2+y2−2x−2y=0{{x}^{2}}+{{y}^{2}}-2x-2y=0 and we have to find the locus of midpoint of all chords of the circle x2+y2−2x−2y=0{{x}^{2}}+{{y}^{2}}-2x-2y=0 such that pair of lines joining (0, 0) and the point of intersection of the chords with the circles make equal angle with x axis.
First of all, let us find out the centre of the circle x2+y2−2x−2y=0{{x}^{2}}+{{y}^{2}}-2x-2y=0. The centre of the circle is the negative of coefficient of x divided by 2 and the y coordinate is equal to negative of coefficient of y divided by 2.
In the below figure, we have drawn a circle x2+y2−2x−2y=0{{x}^{2}}+{{y}^{2}}-2x-2y=0 and a chord in the circle with midpoint as (h, k).

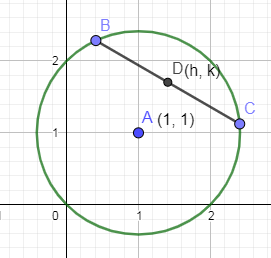
We have given that each of the pair of lines drawn from origin to the extremities of the chord are making an equal angle with the x axis.
If we satisfy the origin (0, 0) in the equation of a circle we get,
(0)2+(0)2−2(0)−2(0)=0 ⇒0+0−0−0=0 ⇒0=0 \begin{aligned} & {{\left( 0 \right)}^{2}}+{{\left( 0 \right)}^{2}}-2\left( 0 \right)-2\left( 0 \right)=0 \\\ & \Rightarrow 0+0-0-0=0 \\\ & \Rightarrow 0=0 \\\ \end{aligned}
Hence, origin lies on the circle.
Now, let us write the equation of chord passing through point D (h, k). We know that equation of chord passing through point (h,k)\left( h,k \right) is equal to:
T=S1T={{S}_{1}}
We have given the equation of circle as x2+y2−2x−2y=0{{x}^{2}}+{{y}^{2}}-2x-2y=0 so S is equal to:
x2+y2−2x−2y{{x}^{2}}+{{y}^{2}}-2x-2y
Substituting the value of x and y as (h,k)\left( h,k \right) in the above expression we get the value of S1{{S}_{1}} as follows:
h2+k2−2h−2k{{h}^{2}}+{{k}^{2}}-2h-2k
Now, the value of T is equal to:
hx+ky−2(x+h2)−2(y+k2) =hx+ky−(x+h)−(y+k) \begin{aligned} & hx+ky-2\left( \dfrac{x+h}{2} \right)-2\left( \dfrac{y+k}{2} \right) \\\ & =hx+ky-\left( x+h \right)-\left( y+k \right) \\\ \end{aligned}
Now, equating T to S1{{S}_{1}} we get,
T=S1 ⇒hx+ky−(x+h)−(y+k)=h2+k2−2h−2k \begin{aligned} & T={{S}_{1}} \\\ & \Rightarrow hx+ky-\left( x+h \right)-\left( y+k \right)={{h}^{2}}+{{k}^{2}}-2h-2k \\\ \end{aligned}
Rearranging the above equation we get,
hx+ky−x−y=h2+k2−2h+h−2k+k ⇒hx+ky−x−y=h2+k2−h−k \begin{aligned} & hx+ky-x-y={{h}^{2}}+{{k}^{2}}-2h+h-2k+k \\\ & \Rightarrow hx+ky-x-y={{h}^{2}}+{{k}^{2}}-h-k \\\ \end{aligned}
Dividing h2+k2−h−k{{h}^{2}}+{{k}^{2}}-h-k on both the sides we get,
hx+ky−x−yh2+k2−h−k=h2+k2−h−kh2+k2−h−k\dfrac{hx+ky-x-y}{{{h}^{2}}+{{k}^{2}}-h-k}=\dfrac{{{h}^{2}}+{{k}^{2}}-h-k}{{{h}^{2}}+{{k}^{2}}-h-k}
⇒hx+ky−x−yh2+k2−h−k=1\Rightarrow \dfrac{hx+ky-x-y}{{{h}^{2}}+{{k}^{2}}-h-k}=1
Now, we are going to homogenize the equation of circle x2+y2−2x−2y=0{{x}^{2}}+{{y}^{2}}-2x-2y=0 as follows:
x2+y2−2(x+y)((hx+ky−x−y)h2+k2−h−k)=0 ⇒(x2+y2)(h2+k2−h−k)−2(x+y)(hx+ky−x−y)=0 ⇒x2(h2+k2−h−k)+y2(h2+k2−h−k)−2hx2−2kxy+2x2+2xy−2hxy−2ky2+2xy+2y2=0 ⇒x2(h2+k2−h−k−2h+2)+y2(h2+k2−h−k−2k+2)+2xy(−h−k+2)=0 \begin{aligned} & {{x}^{2}}+{{y}^{2}}-2\left( x+y \right)\left( \dfrac{\left( hx+ky-x-y \right)}{{{h}^{2}}+{{k}^{2}}-h-k} \right)=0 \\\ & \Rightarrow \left( {{x}^{2}}+{{y}^{2}} \right)\left( {{h}^{2}}+{{k}^{2}}-h-k \right)-2\left( x+y \right)\left( hx+ky-x-y \right)=0 \\\ & \Rightarrow {{x}^{2}}\left( {{h}^{2}}+{{k}^{2}}-h-k \right)+{{y}^{2}}\left( {{h}^{2}}+{{k}^{2}}-h-k \right)-2h{{x}^{2}}-2kxy+2{{x}^{2}}+2xy-2hxy-2k{{y}^{2}}+2xy+2{{y}^{2}}=0 \\\ & \Rightarrow {{x}^{2}}\left( {{h}^{2}}+{{k}^{2}}-h-k-2h+2 \right)+{{y}^{2}}\left( {{h}^{2}}+{{k}^{2}}-h-k-2k+2 \right)+2xy\left( -h-k+2 \right)=0 \\\ \end{aligned}
Hence, we got the above homogenized equation of circle in the form of:
ax2+2hxy+by2=0a{{x}^{2}}+2hxy+b{{y}^{2}}=0
The homogenization of the equation of circle with the equation of chord will give us the pair of lines formed from the origin to the extremities of the chord meaning we get the multiplication of OB and OC.
In the below figure, we have shown the pair of lines by OB and OC.

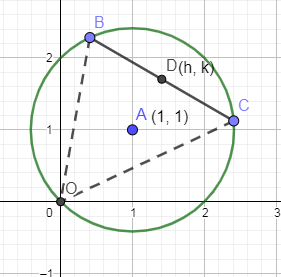
If the slope of these two lines OC and OB are m1&m2{{m}_{1}}\And {{m}_{2}} then sum of m1&m2{{m}_{1}}\And {{m}_{2}} with respect to the homogeneous equation ax2+2hxy+by2=0a{{x}^{2}}+2hxy+b{{y}^{2}}=0 is equal to:
m1+m2=−2hb{{m}_{1}}+{{m}_{2}}=-\dfrac{2h}{b}
Now, using this relation we can find the sum of the slopes for:x2(h2+k2−h−k−2h+2)+y2(h2+k2−h−k−2k+2)+2xy(−h−k+2)=0{{x}^{2}}\left( {{h}^{2}}+{{k}^{2}}-h-k-2h+2 \right)+{{y}^{2}}\left( {{h}^{2}}+{{k}^{2}}-h-k-2k+2 \right)+2xy\left( -h-k+2 \right)=0
m1+m2=−2(−h−k+2)(h2+k2−h−k−2k+2){{m}_{1}}+{{m}_{2}}=-\dfrac{2\left( -h-k+2 \right)}{\left( {{h}^{2}}+{{k}^{2}}-h-k-2k+2 \right)} …………… Eq. (1)
It is also given that these pair of lines are making equal angle with the x axis it means that if one line is making angle θ\theta then the other line is also making the same angle θ\theta but the other angle is written with the negative sign because otherwise it won’t be possible for two lines two be equally inclined with the same axis.
So, we can say the slope of line OC is:
tan⁡θ\tan \theta
Then slope of the line OB is:
tan⁡(−θ) =−tan⁡θ \begin{aligned} & \tan \left( -\theta \right) \\\ & =-\tan \theta \\\ \end{aligned}
Hence, addition of the above slopes is equal to:
m1+m2=tan⁡θ−tan⁡θ=0{{m}_{1}}+{{m}_{2}}=\tan \theta -\tan \theta =0
Substituting the above value of m1+m2{{m}_{1}}+{{m}_{2}} in eq. (1) we get,
0=−2(−h−k+2)(h2+k2−h−k−2k+2)0=-\dfrac{2\left( -h-k+2 \right)}{\left( {{h}^{2}}+{{k}^{2}}-h-k-2k+2 \right)}
Cross multiplying and simplifying the above equation we get,
2(−h−k+2)=0 ⇒(−h−k+2)=0 ⇒h+k=2 \begin{aligned} & 2\left( -h-k+2 \right)=0 \\\ & \Rightarrow \left( -h-k+2 \right)=0 \\\ & \Rightarrow h+k=2 \\\ \end{aligned}
Now, to find the locus of the midpoint of the chord we are going to substitute h by x and k by y.
x+y=2x+y=2
Hence, we got the locus of the midpoint of the all the chords of the circle x2+y2−2x−2y=0{{x}^{2}}+{{y}^{2}}-2x-2y=0 such that pair of lines joining (0, 0) and the point of intersection of the chords with the circles make equal angle with x axis as x+y=2x+y=2.

Note: Whenever if given that you have to find locus of something then basically you have to find the relation between x and y and which you will find by applying the conditions given in the problem like in this problem, we have to the locus of the midpoint of all the chords of the circle x2+y2−2x−2y=0{{x}^{2}}+{{y}^{2}}-2x-2y=0 and the condition is “the pair of lines joining (0, 0) and the point of intersection of the chords with the circles make equal angle with x axis”.