Question

Find the locus of middle points of chords of an ellipse which subtend a right angle at centre.

Answer 1

Write standard equation of chord of contact if middle point is given. Now, form a homogeneous equation of ellipse with the help of chord to get the equation of lines passing through centre joining to points of contact and then use the given condition.

Complete step-by-step answer:
Consider the standard equation of ellipse as $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1-(1)$.

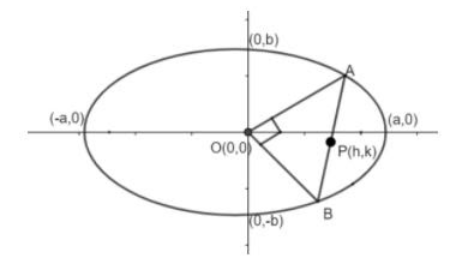
Where A and B points are extremities of chord AB and middle point of that chord.
As we know that if midpoint is given, equation of chord of contact is given by
$T={{S}^{'}}$w.r.t middle point
Where T means writing tangent equation
With respect to middle point by replacing ${{x}^{2}}$by $x{{x}_{1}}$, $y$by $y{{y}_{1}}$, x by $\left( \dfrac{x+{{x}_{1}}}{2} \right)$, y by $\left( \dfrac{y+{{y}_{1}}}{2} \right)$if $\left( {{x}_{1}},{{y}_{1}} \right)$is middle point.
Hence, T can be written by using P (h, k) from ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$as
\Rightarrow $$$$\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}=1
${{S}^{'}}$is represented by direct putting values of $\left( {{x}_{1}},{{y}_{1}} \right)$given in the curve. If $\left( {{x}_{1}},{{y}_{1}} \right)$is a point with respect to which we need to write ${{S}^{'}}$the replace ${{x}^{2}}$by $x_{1}^{2}$, ${{y}^{2}}$by $y_{1}^{2}$, $x$by ${{x}_{1}}$, $y$by ${{y}_{1}}$. Therefore, ${{S}^{'}}$can be written for the ellipse with respect to point P (h, k) (middle point of the chord) as
\Rightarrow $$$${{S}^{'}}=\dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}}-1
Now, from equations (3) and (4) we have values of T and ${{S}^{'}}$we can substitute in equation (2): -

& \dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}-1=\dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}}-1 \\\ & \dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}=\dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \\\ \end{aligned}$$ Now, coming to the second part, that chord is suspending $${{90}^{\circ }}$$to the centre or origin. We know that pair of straight lines passing through which can also termed as homogeneous equation is given as: - $$A{{X}^{2}}+2HXY+B{{Y}^{2}}=0$$ Here, we have an ellipse and a chord through the extremities of which lines to the origin are joined (AO and BO). Now, we can write a homogeneous equation combining the equation of lines AO and BO by homogenization of ellipse with respect to the chord calculated above. We can write equation of ellipse as $$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}={{\left( 1 \right)}^{2}}$$ Equation of chord can be reformed as $$\Rightarrow $$$$\left( \dfrac{\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}}{\dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}}} \right)=1$$ Now replacing $${{\left( 1 \right)}^{2}}$$from the equation of ellipse by using equation of chord to get a homogeneous equation of type $$A{{X}^{2}}+2HXY+B{{Y}^{2}}=0$$which will pass through origin $$\begin{aligned} & \Rightarrow \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=\left( \dfrac{\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}}{\dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}}} \right) \\\ & \Rightarrow {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}\dfrac{{{x}^{2}}}{{{a}^{2}}}+{{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}\dfrac{{{y}^{2}}}{{{b}^{2}}}={{\left( \dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}} \right)}^{2}} \\\ & \Rightarrow {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}\dfrac{{{x}^{2}}}{{{a}^{2}}}+{{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}\dfrac{{{y}^{2}}}{{{b}^{2}}}=\dfrac{{{h}^{2}}{{x}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}{{y}^{2}}}{{{b}^{4}}}+\dfrac{2hkxy}{{{a}^{2}}{{b}^{2}}} \\\ & \Rightarrow \dfrac{{{x}^{2}}}{{{a}^{2}}}\left( {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}-\dfrac{{{h}^{2}}}{{{a}^{2}}} \right)+\dfrac{{{y}^{2}}}{{{b}^{2}}}\left( {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}-\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)-\dfrac{2hkxy}{{{a}^{2}}{{b}^{2}}}=0-(2) \\\ \end{aligned}$$ Now, we can observe that above equation is type of $$\Rightarrow $$$$A{{X}^{2}}+2HXY+B{{Y}^{2}}=0$$ Which is homogeneous passing through origin. As we know that if both lines are perpendicular in $$A{{X}^{2}}+2HXY+B{{Y}^{2}}=0$$, then $$A+B=0-(3)$$ Now, coming to equation (3) both lines OA and OB are perpendicular as given in the problem. Therefore, co-efficient of $${{x}^{2}}$$+ co-efficient of $${{y}^{2}}$$=0 or $$A+B=0$$ Hence, we have $$\begin{aligned} & \Rightarrow A=\left( {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}-\dfrac{{{h}^{2}}}{{{a}^{2}}} \right)\dfrac{1}{{{a}^{2}}} \\\ & \Rightarrow B=\left( {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}-\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)\dfrac{1}{{{b}^{2}}} \\\ \end{aligned}$$ Now, we know that $$A+B=0$$ $$\begin{aligned} & \Rightarrow \left( {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}-\dfrac{{{h}^{2}}}{{{a}^{2}}} \right)\dfrac{1}{{{a}^{2}}}+\left( {{\left( \dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)}^{2}}-\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)\dfrac{1}{{{b}^{2}}}=0 \\\ & \Rightarrow \left( \dfrac{{{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}}{{{a}^{4}}{{b}^{4}}}-\dfrac{{{h}^{2}}}{{{a}^{2}}} \right)\dfrac{1}{{{a}^{2}}}+\left( \dfrac{{{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}}{{{a}^{4}}{{b}^{4}}}-\dfrac{{{k}^{2}}}{{{b}^{2}}} \right)\dfrac{1}{{{b}^{2}}}=0 \\\ & \Rightarrow \dfrac{{{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}}{{{a}^{4}}{{b}^{4}}}+\dfrac{{{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}}{{{a}^{4}}{{b}^{4}}}=\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}} \\\ & \Rightarrow \dfrac{{{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}}{{{a}^{2}}{{b}^{2}}}\left( \dfrac{1}{{{a}^{2}}}+\dfrac{1}{{{b}^{2}}} \right)=\dfrac{{{h}^{2}}{{b}^{4}}+{{k}^{2}}{{a}^{4}}}{{{a}^{4}}{{b}^{4}}} \\\ & \Rightarrow {{\left( {{b}^{2}}{{h}^{2}}+{{a}^{2}}{{k}^{2}} \right)}^{2}}\left( {{a}^{2}}+{{b}^{2}} \right)={{a}^{4}}{{b}^{4}}\left( {{h}^{2}}{{b}^{4}}+{{k}^{2}}{{a}^{4}} \right) \\\ \end{aligned}$$ Replacing h by x & k by y to get locus. $$\left( {{a}^{2}}+{{b}^{2}} \right){{\left( {{b}^{2}}{{x}^{2}}+{{a}^{2}}{{y}^{2}} \right)}^{2}}={{a}^{2}}{{b}^{2}}\left( {{b}^{4}}{{x}^{2}}+{{a}^{4}}{{y}^{2}} \right)$$ **Note:** Equation of chord of contact $$T={{S}^{'}}$$if midpoint is given can be proved by following approach: - Let $$\left( {{x}_{1}},{{y}_{1}} \right)$$and $$\left( {{x}_{2}},{{y}_{2}} \right)$$two points of the extremities of chord of contact and (h, k) is the midpoint of it. Hence, $$h=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$$and $$k=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$$ Now, slope of chord $$=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$$ Since, $$\left( {{x}_{1}},{{y}_{1}} \right)$$and $$\left( {{x}_{2}},{{y}_{2}} \right)$$will pass through $$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$$ Hence, $$\dfrac{x_{1}^{2}}{{{a}^{2}}}+\dfrac{y_{1}^{2}}{{{b}^{2}}}=1$$and $$\dfrac{x_{2}^{2}}{{{a}^{2}}}+\dfrac{y_{2}^{2}}{{{b}^{2}}}=1$$ On subtracting both the equations we get, $$\begin{aligned} & \Rightarrow \dfrac{1}{{{a}^{2}}}\left( {{x}_{1}}-{{x}_{2}} \right)\left( {{x}_{1}}+{{x}_{2}} \right)+\dfrac{1}{{{b}^{2}}}\left( {{y}_{1}}-{{y}_{2}} \right)\left( {{y}_{1}}+{{y}_{2}} \right)=0 \\\ & \Rightarrow \dfrac{1}{{{a}^{2}}}\left( {{x}_{1}}-{{x}_{2}} \right)\left( {{x}_{1}}+{{x}_{2}} \right)=\dfrac{-1}{{{b}^{2}}}\left( {{y}_{1}}-{{y}_{2}} \right)\left( {{y}_{1}}+{{y}_{2}} \right) \\\ & \Rightarrow \dfrac{-{{b}^{2}}}{{{a}^{2}}}\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{{{y}_{1}}+{{y}_{2}}} \right)=\dfrac{{{y}_{1}}-{{y}_{2}}}{{{x}_{1}}-{{x}_{2}}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \\\ \end{aligned}$$ Hence, using the above relation, we can rewrite slope of chord as $$\dfrac{-{{b}^{2}}}{{{a}^{2}}}\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{{{y}_{1}}+{{y}_{2}}} \right)$$or $$\dfrac{-{{b}^{2}}}{{{a}^{2}}}.\dfrac{h}{k}$$. Equation of chord is $$\Rightarrow $$$$y-k=\dfrac{-{{b}^{2}}}{{{a}^{2}}}.\dfrac{h}{k}(x-h)$$ On simplifying the above relation we can write $$\begin{aligned} & \Rightarrow \dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}-1=\dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}}-1 \\\ & \Rightarrow T={{S}^{'}} \\\ \end{aligned}$$ But using the above relation directly to any conic will give the right solution and makes the solution easier and flexible. Another approach for this question would be that we can suppose points A and B in parametric form $$\left( a\cos {{\theta }_{1}},b\sin {{\theta }_{1}} \right)$$and $$\left( a\cos {{\theta }_{2}},b\sin {{\theta }_{2}} \right)$$and write $$h=\dfrac{a\left( \cos {{\theta }_{1}}+\cos {{\theta }_{2}} \right)}{2},k=\dfrac{b\left( \sin {{\theta }_{1}}+\sin {{\theta }_{2}} \right)}{2}$$. Now, $$OA\bot OB$$then Slope of OA $$\times $$slope of OB=-1 $$\dfrac{b}{a}\dfrac{\sin {{\theta }_{1}}}{\cos {{\theta }_{1}}}\times \dfrac{b}{a}\dfrac{\sin {{\theta }_{2}}}{\cos {{\theta }_{2}}}=-1$$ Using the above relation, try to write relation between h and k, by eliminating $${{\theta }_{1}}$$and $${{\theta }_{2}}$$. Calculation is an important part of the solution as well.