Question

Find the locus of intersection of tangents which meet at a given angle $\alpha$with ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.

Answer 1

Hint: Use the standard equation of tangent for ellipse for tangent $y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}$, then form a quadratic in ‘m’ and use formula $\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$to get locus.

Complete step-by-step answer:
We have considered ellipse equation as \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\left\\{ \because a>b \right\\}

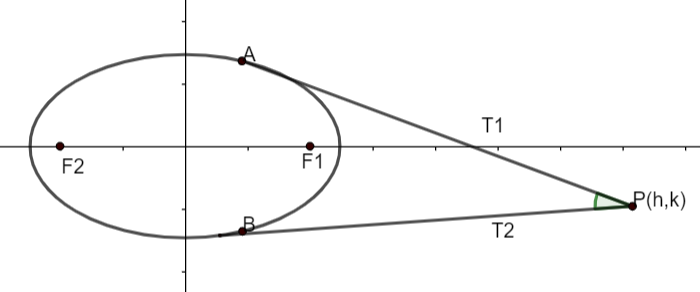
Let the point of intersection be P (h, k).
As we know,
Equation to the tangent $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$in slope form is
$y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}$
As, this equation will pass through (h, k).
Hence,
$k=mh\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}$
$k-mh=\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}$
Squaring both sides

& {{\left( k-mh \right)}^{2}}={{a}^{2}}{{m}^{2}}+{{b}^{2}} \\\ & {{k}^{2}}+{{m}^{2}}{{h}^{2}}-2kmh={{a}^{2}}{{m}^{2}}+{{b}^{2}} \\\ & \left( {{h}^{2}}-{{a}^{2}} \right){{m}^{2}}-2mhk+{{k}^{2}}-{{b}^{2}}=0-(1)\left\\{ \because {{\left( APB \right)}^{2}}={{A}^{2}}+{{B}^{2}}+2AB \right\\} \\\ \end{aligned}$$ This equation is quadratic in m and has two roots. Let’s suppose $${{m}_{1}}$$and $${{m}_{2}}$$which are slopes of $${{T}_{1}}$$and $${{T}_{2}}$$tangents shown in diagram: - As, if we have quadratic $$A{{X}^{2}}+BX+C=0$$ Then sum of roots $$=\dfrac{-B}{A}$$ Product of roots $$=\dfrac{C}{A}$$ Hence, from the equation (1) $$\begin{aligned} & {{m}_{1}}+{{m}_{2}}=\dfrac{2hk}{{{h}^{2}}-{{a}^{2}}} \\\ & {{m}_{1}}.{{m}_{2}}=\dfrac{{{k}^{2}}-{{b}^{2}}}{{{h}^{2}}-{{a}^{2}}} \\\ \end{aligned}$$ As, $$\tan \alpha =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$$  If slope of two lines are given then $$\tan \alpha =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$$as $$\alpha $$is angle between two lines. $$\begin{aligned} & {{\tan }^{2}}\alpha =\dfrac{{{\left( {{m}_{1}}-{{m}_{2}} \right)}^{2}}}{{{\left( 1+{{m}_{1}}{{m}_{2}} \right)}^{2}}} \\\ & {{\tan }^{2}}\alpha =\dfrac{{{\left( {{m}_{1}}+{{m}_{2}} \right)}^{2}}-4{{m}_{1}}{{m}_{2}}}{{{\left( 1+{{m}_{1}}{{m}_{2}} \right)}^{2}}}\left\\{ \because {{\left( a-b \right)}^{2}}={{\left( a+b \right)}^{2}}-4ab \right\\} \\\ & {{\tan }^{2}}\alpha =\dfrac{{{\left( \dfrac{2hk}{{{h}^{2}}-{{a}^{2}}} \right)}^{2}}-4\left( \dfrac{{{k}^{2}}-{{b}^{2}}}{{{h}^{2}}-{{a}^{2}}} \right)}{{{\left( 1+\dfrac{{{k}^{2}}-{{b}^{2}}}{{{h}^{2}}-{{a}^{2}}} \right)}^{2}}} \\\ & {{\tan }^{2}}\alpha =\dfrac{4{{h}^{2}}{{k}^{2}}-4\left( {{h}^{2}}-{{a}^{2}} \right)\left( {{k}^{2}}-{{b}^{2}} \right)}{{{\left( {{h}^{2}}+{{k}^{2}}-{{a}^{2}}-{{b}^{2}} \right)}^{2}}} \\\ \end{aligned}$$ Replacing (h, k) by (x, y) to get locus: - $${{\left( {{x}^{2}}+{{y}^{2}}-{{a}^{2}}-{{b}^{2}} \right)}^{2}}=4{{\cot }^{2}}\alpha \left( {{x}^{2}}{{b}^{2}}+{{a}^{2}}{{y}^{2}}-{{a}^{2}} \right)$$is required locus. Note: Using formula $$\tan \alpha =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$$and writing relations from tangent equation $$y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}$$or $${{\left( y-mx \right)}^{2}}={{a}^{2}}{{m}^{2}}+{{b}^{2}}$$which is quadratic in m and using relations of roots with coefficients of quadratic is a key point of this equation. We can use the direct formula of tangent of ellipse i.e. $$y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}$$standard equation $$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$$which can be proved by following approach: -  Now, y=mx + c and $$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$$have only one intersection point (touching the ellipse). So, if we substitute y=mx + c in $$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$$at place of y then we will get quadratic in x which should have one solution (as tangent and ellipse have only one intersection point). Then we will get $$c=\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}$$by making decrement of that quadratic to 0. Second approach to the solution can be: - We can suppose A and B points as a parametric coordinates of ellipse as $$A\left( a\sin {{\theta }_{1}},b\cos {{\theta }_{1}} \right)\And B\left( a\sin {{\theta }_{2}},b\cos {{\theta }_{2}} \right)$$and write tangent equations from A and B as ‘T=0’ or $$\begin{aligned} & \dfrac{a\sin {{\theta }_{1}}}{a}+\dfrac{y\cos {{\theta }_{1}}}{b}=1 \\\ & \dfrac{a\sin {{\theta }_{2}}}{a}+\dfrac{y\cos {{\theta }_{2}}}{b}=1 \\\ \end{aligned}$$ And then find the intersection of above two tangent and trying to eliminate $${{\theta }_{1}}\And {{\theta }_{2}}$$by using the given condition with using same formula $$\tan \alpha =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$$. Where $${{m}_{1}}=\dfrac{\dfrac{-\sin {{\theta }_{1}}}{a}}{\dfrac{\cos {{\theta }_{1}}}{b}}=\dfrac{-b\sin {{\theta }_{1}}}{a\cos {{\theta }_{1}}}$$ $${{m}_{2}}=\dfrac{\dfrac{-\sin {{\theta }_{2}}}{a}}{\dfrac{\cos {{\theta }_{2}}}{b}}=\dfrac{-b\sin {{\theta }_{2}}}{a\cos {{\theta }_{2}}}$$