Question

Find the locus of intersection of tangents if the sum of eccentric angles of their points of contact be equal to a constant angle $2\alpha$ .

Answer 1

Use the standard equation of tangent for ellipse for tangent $y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}$ , then form a quadratic in ‘m’ and use the given condition to get locus.

Complete step-by-step answer:
Here, we have given a ellipse is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1-(1)$ .
Let eccentric angles of two points A and B are ${{\theta }_{1}}$ and ${{\theta }_{2}}$ as shown in figure.

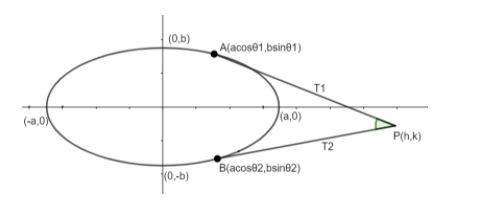
Where A and B are parametric coordinates.
Eccentric angle is the angle between the major axis and line joining the circle at a point where perpendicular from any point to the major axis of ellipse is extended to the circle as shown in diagram.

Let us suppose the intersection of two tangents ${{T}_{1}}$ and ${{T}_{2}}$ is P (h, k) of which we need to find locus. It is given that the sum of eccentric angles of point A and B is $2\alpha$ .
${{\theta }_{1}}+{{\theta }_{2}}=2\alpha -(2)$
Let us find the slopes of both tangents ${{T}_{1}}$ and ${{T}_{2}}$ .
We can write equation of tangent with respect to any point of contact of tangent $({{x}_{1}},{{y}_{1}})$ to an ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ as
$\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{{{b}^{2}}}=1-(3)$
Now, we have $A\left( a\cos {{\theta }_{1}},b\sin {{\theta }_{1}} \right)$ and $B\left( a\cos {{\theta }_{2}},b\sin {{\theta }_{2}} \right)$ coordinates.
So, tangent equations with respect to A by using equation (3) is
$\dfrac{xa\cos {{\theta }_{1}}}{{{a}^{2}}}+\dfrac{yb\sin {{\theta }_{1}}}{{{b}^{2}}}=1$
Or
$\Rightarrow$ $\dfrac{x\cos {{\theta }_{1}}}{a}+\dfrac{y\sin {{\theta }_{1}}}{b}=1-(4)$
Similarly, equation of tangent ${{T}_{2}}$ is
$\Rightarrow$ $\dfrac{x\cos {{\theta }_{2}}}{a}+\dfrac{y\sin {{\theta }_{2}}}{b}=1-(5)$
As we know that slope of any line can be determined by comparing it with $y=mx+c$ equation.
We can write equation of tangent ${{T}_{1}}$ as
$\Rightarrow$ $y=\dfrac{-xb}{a}\dfrac{\cos {{\theta }_{1}}}{\sin {{\theta }_{1}}}+\dfrac{b}{\sin {{\theta }_{1}}}$
Hence, slope of tangent ${{T}_{1}}$ as
$\Rightarrow$ ${{m}_{1}}=\dfrac{-b\cos {{\theta }_{1}}}{a\sin {{\theta }_{1}}}-(6)$ (Let slope of ${{T}_{1}}$ is ${{m}_{1}}$ )
Hence, slope of tangent ${{T}_{2}}$ as
$\Rightarrow$ ${{m}_{2}}=\dfrac{-b\cos {{\theta }_{2}}}{a\sin {{\theta }_{2}}}-(7)$ (Let slope of ${{T}_{2}}$ is ${{m}_{1}}$ )
As we know that equation of tangent in slope from drawn from an external point is
$y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}$ for ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ .
As, tangent is drawn from (h, k) or tangents will pass through (h, k). Hence, above equation of tangent will pass through (h, k).

& \Rightarrow k=mh\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}} \\\ & k-mh=\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}} \\\ \end{aligned}$$ Squaring both sides, we can get $$\begin{aligned} & {{k}^{2}}+{{m}^{2}}{{h}^{2}}-2mhk={{a}^{2}}{{m}^{2}}+{{b}^{2}} \\\ & {{m}^{2}}\left( {{h}^{2}}-{{a}^{2}} \right)-2mhk+{{k}^{2}}-{{b}^{2}}=0 \\\ \end{aligned}$$ This equation is a quadratic in ‘m’ have two roots $${{m}_{1}}$$ and $${{m}_{1}}$$ which are slopes of tangents $${{T}_{1}}$$ and $${{T}_{2}}$$ . As we already new the know the relation between roots and coefficients of quadratic equation as Sum of roots $$=\dfrac{-B}{A}$$ Product of roots $$=\dfrac{C}{A}$$ In general quadratic $$A{{X}^{2}}+BX+C=0$$ Hence, we can write the relation of $${{m}_{1}}$$ and $${{m}_{2}}$$ with coefficients of calculated quadratic. $$\begin{aligned} & {{m}_{1}}+{{m}_{2}}=\dfrac{2hk}{{{h}^{2}}-{{a}^{2}}}-(8) \\\ & {{m}_{1}}{{m}_{2}}=\dfrac{{{k}^{2}}-{{b}^{2}}}{{{h}^{2}}-{{a}^{2}}}-(8) \\\ \end{aligned}$$ We have already calculated slopes of tangents $${{T}_{1}}$$ and $${{T}_{2}}$$ as $$\begin{aligned} & {{m}_{1}}=\dfrac{-b\cos {{\theta }_{1}}}{a\sin {{\theta }_{1}}} \\\ & {{m}_{2}}=\dfrac{-b\cos {{\theta }_{2}}}{a\sin {{\theta }_{2}}} \\\ \end{aligned}$$ Putting values of $${{m}_{1}}$$ and $${{m}_{2}}$$ in equation (8), we get $$\Rightarrow $$ $$\dfrac{-b}{a}\left( \dfrac{\cos {{\theta }_{1}}}{\sin {{\theta }_{1}}}+\dfrac{\cos {{\theta }_{2}}}{\sin {{\theta }_{2}}} \right)=\dfrac{2hk}{{{h}^{2}}-{{a}^{2}}}-(9)$$ And $$\begin{aligned} & \left( \dfrac{-b}{a}.\dfrac{\cos {{\theta }_{1}}}{\sin {{\theta }_{1}}} \right)\left( \dfrac{-b}{a} \right)\dfrac{\cos {{\theta }_{2}}}{\sin {{\theta }_{2}}}=\dfrac{{{k}^{2}}-{{b}^{2}}}{{{h}^{2}}-{{a}^{2}}} \\\ & \dfrac{{{b}^{2}}}{{{a}^{2}}}\dfrac{\cos {{\theta }_{1}}\cos {{\theta }_{2}}}{\sin {{\theta }_{1}}\sin {{\theta }_{2}}}=\dfrac{{{k}^{2}}-{{b}^{2}}}{{{h}^{2}}-{{a}^{2}}}-(10) \\\ \end{aligned}$$ Equation (9) and (10) can also be written as $$\Rightarrow $$ $$\dfrac{{{b}^{2}}}{{{a}^{2}}}\left( \cot {{\theta }_{1}}+\cot {{\theta }_{2}} \right)=\dfrac{2hk}{{{h}^{2}}-{{a}^{2}}}$$ And $$\Rightarrow $$ $$\dfrac{{{b}^{2}}}{{{h}^{2}}}\cot {{\theta }_{1}}\cot {{\theta }_{2}}=\dfrac{{{k}^{2}}-{{b}^{2}}}{{{h}^{2}}-{{a}^{2}}}$$ Now, we have formula of $$\cot \left( {{\theta }_{1}}+{{\theta }_{2}} \right)$$ as $$\cot \left( {{\theta }_{1}}+{{\theta }_{2}} \right)=\dfrac{\cot {{\theta }_{1}}.\cot {{\theta }_{2}}-1}{\cot {{\theta }_{1}}+\cot {{\theta }_{2}}}$$ Putting the values of $$\cot {{\theta }_{1}}\cot {{\theta }_{2}}$$ and $$\cot {{\theta }_{1}}+\cot {{\theta }_{2}}$$ in above equation as $$\Rightarrow $$ $$\cot \left( {{\theta }_{1}}+{{\theta }_{2}} \right)=\dfrac{\dfrac{\left( {{k}^{2}}-{{b}^{2}} \right)}{\left( {{h}^{2}}-{{a}^{2}} \right)}\dfrac{{{a}^{2}}}{{{b}^{2}}}-1}{\left( \dfrac{2hk}{{{h}^{2}}-{{a}^{2}}} \right)\times \left( \dfrac{-b}{a} \right)}$$ Now, from equation (2) we have $${{\theta }_{1}}+{{\theta }_{2}}=2\alpha $$ Therefore, $$\Rightarrow $$ $$\begin{aligned} & \cot 2\alpha =\dfrac{\dfrac{{{a}^{2}}\left( {{k}^{2}}-{{b}^{2}} \right)-{{b}^{2}}\left( {{h}^{2}}-{{a}^{2}} \right)}{{{b}^{2}}\left( {{h}^{2}}-{{a}^{2}} \right)}}{\dfrac{-2bhk}{a\left( {{h}^{2}}-{{a}^{2}} \right)}} \\\ & \cot 2\alpha =\dfrac{{{a}^{2}}{{k}^{2}}-{{b}^{2}}{{a}^{2}}-{{b}^{2}}{{h}^{2}}+{{a}^{2}}{{b}^{2}}}{{{b}^{2}}\left( {{h}^{2}}-{{a}^{2}} \right)}\times \dfrac{-a\left( {{h}^{2}}-{{a}^{2}} \right)}{2bhk} \\\ & \cot 2\alpha =\dfrac{-\left( {{a}^{2}}{{k}^{2}}-{{b}^{2}}{{h}^{2}} \right)a}{2{{b}^{3}}hk} \\\ \end{aligned}$$ Replacing (h, k) with (x, y) to get locus: - $$2{{b}^{3}}xy\cot 2\alpha ={{b}^{2}}{{x}^{2}}a-{{b}^{2}}{{x}^{2}}a-{{a}^{3}}{{y}^{2}}$$ is required locus. **Note:** Elimination of $${{\theta }_{1}}$$ and $${{\theta }_{2}}$$ which are eccentric angles of point A and B is a key point of this question. Directly using the formula of tangent to an ellipse whose slope is given, solved the problem easily. Using formulae in conic sections always helps and make the solution easier. Here, we can use direct formula of tangent of ellipse i.e. $$y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}$$ for standard ellipse $$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$$ which can be proved by following approach: -  Now $$y=mx+c$$ and $$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$$ have only are intersection point (touching the ellipse). So, if we substitute $$y=mx+c$$ in $$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$$ at place of y then we will get quadratic in x which should -d have one solution (as tangent and ellipse have only one intersection point). Then we will get $$c=\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}$$ by making decrement of that quadratic to 0. One can get confuse with formula of tangent with point given on any curve i.e. T=0. General way of writing tangent equation; if $$({{x}_{1}},{{y}_{1}})$$ point lies on curve c then we need to replace $${{x}^{2}}$$ by $$x{{x}_{1}}$$ , $${{y}^{2}}$$ by $$y{{y}_{1}}$$ , $$x$$ by $$\left( \dfrac{x+{{x}_{1}}}{2} \right)$$ , $$y$$ by $$\left( \dfrac{y+{{y}_{1}}}{2} \right)$$ .