Question

Find the locus of intersection of tangents if the sum of the ordinates of the points of contact be equal to b in ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.

Answer 1

Hint: Write down the standard equation of chord of contact. And suppose parametric coordinates for both points of contact of contact. Write down line passes through it (chord of contact). Compare both lines as they represent the same line.

Complete step-by-step answer:

We have given equation of ellipse as $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1-(1)$
Let us suppose two points on ellipse $A(a\cos \theta ,b\sin \theta )$ and $B(a\cos \varphi ,b\sin \varphi )$ in parametric form.

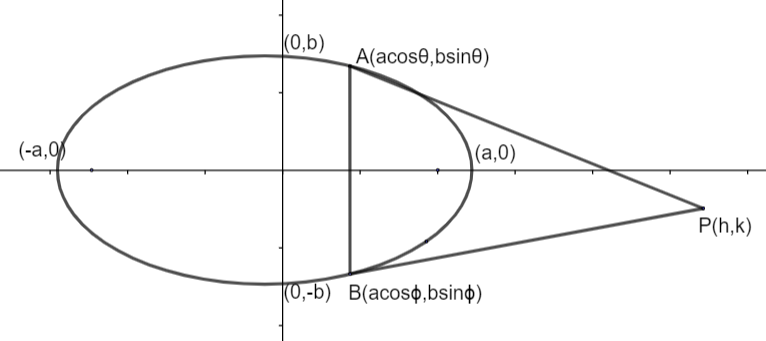
We have given that sum of ordinates of points of contacts of tangents is b i.e.

& b\sin \theta +b\sin \varphi =b \\\ & \sin \theta +\sin \varphi =1 \\\ \end{aligned}$$ We know that $$\sin C+\sin D=2\sin \dfrac{C+D}{2}\cos \dfrac{C-D}{2}$$ Therefore, we can write the above equations as $$2\sin \dfrac{\theta +\varphi }{2}\cos \dfrac{\theta -\varphi }{2}=1-(2)$$ Let us write equation of chord through A and B: Equation of a line with two points given $$({{x}_{1}},{{y}_{1}})$$and $$({{x}_{2}},{{y}_{2}})$$ is $$y-{{y}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)$$ Equation of chord AB is $$y-b\sin \theta =\dfrac{b\left( \sin \theta -\sin \phi \right)}{a\left( \cos \theta -\cos \phi \right)}\left( x-a\cos \theta \right)$$ We know: - $$\begin{aligned} & \sin C-\sin D=2\sin \dfrac{C-D}{2}\cos \dfrac{C+D}{2} \\\ & \cos C-\cos D=-2\sin \dfrac{C-D}{2}\sin \dfrac{C+D}{2} \\\ \end{aligned}$$ We can rewrite the equation of chord AB as, $$\begin{aligned} & y-b\sin \theta =\dfrac{2b\left( \sin \dfrac{\theta -\phi }{2}\cos \dfrac{\theta +\phi }{2} \right)}{-2a\left( \sin \dfrac{\theta -\phi }{2}\sin \dfrac{\theta +\phi }{2} \right)}\left( x-a\cos \theta \right) \\\ & y-b\sin \theta =\dfrac{-b\cos \dfrac{\theta +\phi }{2}}{a\sin \left( \dfrac{\theta +\phi }{2} \right)}\left( x-a\cos \theta \right) \\\ & ay\sin \dfrac{\theta +\phi }{2}-ab\sin \theta \sin \dfrac{\theta +\phi }{2}=-bx\cos \left( \dfrac{\theta +\phi }{2} \right)+ab\cos \theta \cos \dfrac{\theta +\phi }{2} \\\ & bx\cos \left( \dfrac{\theta +\phi }{2} \right)+ay\sin \dfrac{\theta +\phi }{2}=ab\left( +\sin \theta \sin \dfrac{\theta +\phi }{2}+\cos \theta \cos \dfrac{\theta +\phi }{2} \right) \\\ & bx\cos \dfrac{\theta +\phi }{2}+ay\sin \dfrac{\theta +\phi }{2}=ab\left( \cos \dfrac{\theta -\phi }{2} \right)\left\\{ \because \cos \left( A-B \right)=\cos A.\cos B+\sin A.\sin B \right\\} \\\ \end{aligned}$$ or $$\dfrac{x}{a}\left( \dfrac{\cos \dfrac{\theta +\phi }{2}}{\cos \dfrac{\theta -\phi }{2}} \right)+\dfrac{y}{b}\dfrac{\sin \dfrac{\theta +\phi }{2}}{\cos \dfrac{\theta -\phi }{2}}=1-(3)$$ We can write the equation of chord of contact using the co-ordinate (h, k) from where tangents are drawn to the ellipse as T=0 with respect to (h, k). Hence, equation of chord w.r.t (h, k) to $$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$$ is $$\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}=1-(4)$$ As we can observe the equation (3) and (4) represents the same equation of line. Hence, ratios of terms are equal. $$\dfrac{\dfrac{hx}{{{a}^{2}}}}{\dfrac{x}{a}\left( \dfrac{\cos \dfrac{\theta +\varphi }{2}}{\cos \dfrac{\theta -\varphi }{2}} \right)}=\dfrac{\dfrac{ky}{{{b}^{2}}}}{\dfrac{y}{b}\left( \dfrac{\sin \dfrac{\theta +\varphi }{2}}{\sin \dfrac{\theta -\varphi }{2}} \right)}=\dfrac{1}{1}$$ $$\dfrac{h}{{{a}^{2}}}=\dfrac{1}{a}\dfrac{\cos \left( \dfrac{\theta +\phi }{2} \right)}{\cos \left( \dfrac{\theta -\phi }{2} \right)}$$ And $$\dfrac{k}{{{b}^{2}}}=\dfrac{1}{b}\dfrac{\sin \left( \dfrac{\theta +\phi }{2} \right)}{\cos \left( \dfrac{\theta -\phi }{2} \right)}-(4)$$ Now, using the relation of equation (2) $$\cos \dfrac{\theta -\varphi }{2}=\dfrac{1}{2\sin \left( \dfrac{\theta +\varphi }{2} \right)}$$ Hence, values of $$\dfrac{h}{{{a}^{2}}}$$and $$\dfrac{k}{{{b}^{2}}}$$ can be written as, Given that the sum of ordinates of A & B is b. Hence, $$\begin{aligned} & \dfrac{h}{{{a}^{2}}}=\dfrac{1}{a}\dfrac{\cos \left( \dfrac{\theta +\varphi }{2} \right)}{\dfrac{1}{2\sin \left( \dfrac{\theta +\varphi }{2} \right)}}=\dfrac{2}{a}\cos \left( \dfrac{\theta +\varphi }{2} \right)\sin \left( \dfrac{\theta +\varphi }{2} \right) \\\ & h=2a\cos \left( \dfrac{\theta +\varphi }{2} \right)\sin \left( \dfrac{\theta +\varphi }{2} \right)-(5) \\\ & \dfrac{k}{{{b}^{2}}}=\dfrac{1}{b}\dfrac{\sin \left( \dfrac{\theta +\varphi }{2} \right)}{\dfrac{1}{2\sin \left( \dfrac{\theta +\varphi }{2} \right)}}=\dfrac{2}{b}{{\sin }^{2}}\left( \dfrac{\theta +\varphi }{2} \right) \\\ & k=2b{{\sin }^{2}}\left( \dfrac{\theta +\varphi }{2} \right)-(6) \\\ \end{aligned}$$ From the equation (6), we can write the values of $${{\sin }^{2}}\left( \dfrac{\theta +\varphi }{2} \right)$$and $${{\cos }^{2}}\left( \dfrac{\theta +\varphi }{2} \right)$$ in following way:- $$\begin{aligned} & {{\sin }^{2}}\left( \dfrac{\theta +\varphi }{2} \right)=\dfrac{k}{2b} \\\ & {{\cos }^{2}}\left( \dfrac{\theta +\varphi }{2} \right)=1-\dfrac{k}{2b}\left( \because {{\sin }^{2}}\theta +{{\cos }^{2}}=1 \right) \\\ & \\\ \end{aligned}$$ Putting the values of $${{\sin }^{2}}\left( \dfrac{\theta +\varphi }{2} \right)$$and $${{\cos }^{2}}\left( \dfrac{\theta +\varphi }{2} \right)$$with equation (6) as: -$$\begin{aligned} & {{h}^{2}}=4{{a}^{2}}{{\cos }^{2}}\left( \dfrac{\theta +\varphi }{2} \right){{\sin }^{2}}\left( \dfrac{\theta +\varphi }{2} \right) \\\ & {{h}^{2}}=4{{a}^{2}}\left( 1-\dfrac{k}{2b} \right)\left( \dfrac{k}{2b} \right) \\\ & {{h}^{2}}=\dfrac{{{a}^{2}}}{{{b}^{2}}}\left( 2b-k \right)k \\\ \end{aligned}$$ Replacing (h, k) by (x, y) we can write the above equation as $${{x}^{2}}{{b}^{2}}={{a}^{2}}\left( 2b-y \right)y$$ $${{b}^{2}}{{x}^{2}}+{{a}^{2}}{{y}^{2}}=2{{a}^{2}}by$$ (Required locus) Note: Elimination of $$\theta $$ and $$\varphi $$ in the solution is the key point of the question by using the given condition $$\sin \theta +\sin \varphi =1$$. Another typical approach for this question would be to write the tangents through $$A(a\cos \theta, b\sin \theta )$$ and $$B(a\cos \varphi ,b\sin \varphi )$$. Then find the intersection of them and equate the coordinate to h and k, and eliminate $$\theta $$ and $$\varphi $$ with the given condition $$\sin \theta +\sin \varphi =1$$. One can get confuse with the formula of tangent with point given on any curve i.e. T=0. General way of writing tangent equation is, If $$\left( {{x}_{1}},{{y}_{1}} \right)$$ point lies on curve C then we need to replace $${{x}^{2}}$$ by $$x{{x}_{1}}$$ $${{y}^{2}}$$ by $$y{{y}_{1}}$$ x by $$\left( \dfrac{x+{{x}_{1}}}{2} \right)$$ y by $$\left( \dfrac{y+{{y}_{1}}}{2} \right)$$