Question

Find the locus of a point which is such that two of the normal drawn from it to the parabola are at right angles.

Answer 1

Find the slope of tangent by ${{\left. \dfrac{dy}{dx} \right|}_{\left( {{x}_{1}},{{y}_{1}} \right)}}$, where y is a given function and $\left( {{x}_{1}},{{y}_{1}} \right)$ is a point of tangency and hence, get slope of normal by relation
Product of slopes of two perpendicular lines = - 1
Suppose P and Q as parametric coordinates on parabola ${{y}^{2}}=4ax$. Parametric coordinate on this parabola is given as $\left( a{{t}^{2}},2at \right)$.

Complete step-by-step answer:
Let us suppose the equation of the parabola be ${{y}^{2}}=4ax$.
${{y}^{2}}=4ax$…………….. (i)
Now, we know parametric coordinates on parabola ${{y}^{2}}=4ax$can be given as $\left( a{{t}^{2}},2at \right)$. So, let two normal drawn to the parabola from a point are $\left( a{{t}^{2}},2at \right),\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$ and coordinates of point is (h, k) and hence, we need to determine the locus of point (h, k). So, we can draw diagram as

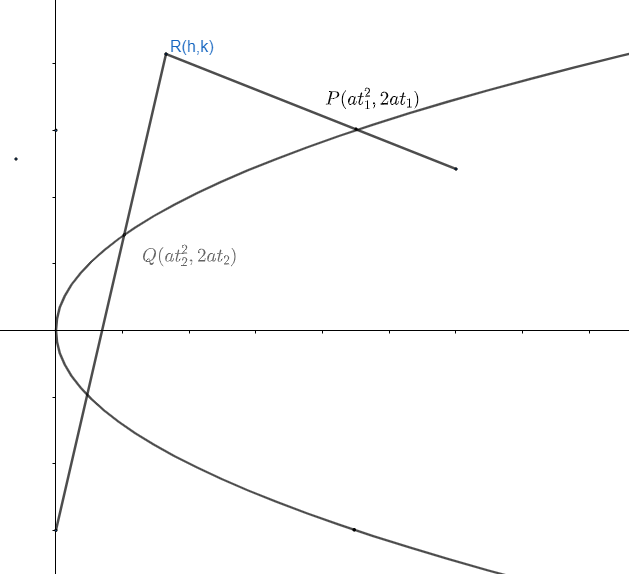
Hence, R is a point from where normal to the parabola at points P and Q are drawn and $\angle QRP\to {{90}^{\circ }}$ i.e. normal are perpendicular to each other. So, we have $P\left( h,k \right),P\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right),Q\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$ …………….. (ii)
As, we know slope of any tangent at any point $\left( {{x}_{1}},{{y}_{1}} \right)$ for any curve y = f(x) is given by ${{\left. \dfrac{dy}{dx} \right|}_{\left( {{x}_{1}},{{y}_{1}} \right)}}$.
So, slope of tangent through P can be given by differentiating the given curve ${{y}^{2}}=4ax$ and hence putting the coordinate of P to it.
So, we can differentiate ${{y}^{2}}=4ax$as $\dfrac{d}{dx}{{y}^{2}}=\dfrac{d}{dx}=4ax$
We know $\dfrac{d}{dx}{{x}^{n}}=n{{x}^{n-1}}$
So, we get
$\begin{aligned} & 2y\dfrac{dy}{dx}=4a \\\ & \dfrac{dy}{dx}=\dfrac{2a}{y} \\\ \end{aligned}$
So, slope at P is
${{\left. \dfrac{dy}{dx} \right|}_{\left( a{{t}^{2}},2a{{t}_{1}} \right)}}=\dfrac{2a}{2a{{t}_{1}}}=\dfrac{1}{{{t}_{1}}}$
And similarly slope at Q is
${{\left. \dfrac{dy}{dx} \right|}_{\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)}}=\dfrac{2a}{2a{{t}_{2}}}=\dfrac{1}{{{t}_{2}}}$
And as we know tangent at any point of the curve is perpendicular to the normal at the same point. And hence, as we know, the product of slopes of two perpendicular lines I ‘-1’. So, we can get reaction as
${{m}_{1}}{{m}_{2}}=-1$ …………….. (iii)
Where ${{m}_{1}},{{m}_{2}}$are slopes of both lines point P so, slopes of normal at point P can be given as
$\begin{aligned} & \left( \text{slope of normal at P} \right)\text{ }\\!\\!\times\\!\\!\text{ }\left( \text{slope of tangent at P} \right)\text{ = - 1} \\\ & \left( \text{slope of normal at P} \right)\text{ }\\!\\!\times\\!\\!\text{ }\dfrac{\text{1}}{{{\text{t}}_{\text{1}}}}\text{=-1} \\\ & \text{slope of normal at P = - }{{\text{t}}_{1}} \\\ \end{aligned}$
Similarly,
$\text{slope of normal at Q = - }{{\text{t}}_{2}}$
Now, we know equation of a line passing through point $\left( {{x}_{1}},{{y}_{1}} \right)$and have slope ‘m’ can be given as
$y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$ ……………. (iv)
So, normal at P can be given as
$\begin{aligned} & y-2a{{t}_{1}}=-{{t}_{1}}\left( x-a{{t}_{1}}^{2} \right) \\\ & y-2a{{t}_{1}}=-{{t}_{1}}x+a{{t}_{1}}^{3} \\\ \end{aligned}$
${{t}_{1}}x+y-2a{{t}_{1}}-a{{t}_{1}}^{3}=0$…………. (v)
Similarly, normal at Q can be given as
$\begin{aligned} & y-2a{{t}_{2}}=-{{t}_{2}}\left( x-a{{t}_{2}}^{2} \right) \\\ & y-2a{{t}_{2}}=-{{t}_{2}}x+a{{t}_{2}}^{3} \\\ \end{aligned}$
${{t}_{2}}x+y-2a{{t}_{2}}-a{{t}_{2}}^{3}=0$ …………… (vi)
Now, subtract equation (v) and (vi) to get value of ‘x’ coordinate of point R, so, we get

& \left( {{t}_{2}}x+y-2a{{t}_{2}}-a{{t}_{2}}^{3} \right)-\left( {{t}_{1}}x+y-2a{{t}_{1}}-a{{t}_{1}}^{3} \right)=0 \\\ & x\left( {{t}_{2}}-{{t}_{1}} \right)-2a\left( {{t}_{2}}-{{t}_{1}} \right)-a\left( {{t}_{2}}^{3}-{{t}_{2}}^{3} \right)=0 \\\ \end{aligned}$$ We know ${{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+{{b}^{2}}+ab \right)$ $$\begin{aligned} & \left( {{t}_{2}}-{{t}_{1}} \right)x-2a\left( {{t}_{2}}-{{t}_{1}} \right)-a\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}^{2}}_{2}+{{t}^{2}}_{1}+{{t}_{1}}{{t}_{2}} \right)=0 \\\ & \left( {{t}_{2}}-{{t}_{1}} \right)\left[ x-2a-a\left( {{t}^{2}}_{2}+{{t}^{2}}_{1}+{{t}_{1}}{{t}_{2}} \right) \right]=0 \\\ \end{aligned}$$ We get $$\begin{aligned} & {{t}_{2}}-{{t}_{1}}=0,x-2a-a\left( {{t}^{2}}_{2}+{{t}^{2}}_{1}+{{t}_{1}}{{t}_{2}} \right)=0 \\\ & {{t}_{1}}={{t}_{2}},x-2a-a\left( {{t}^{2}}_{2}+{{t}^{2}}_{1}+{{t}_{1}}{{t}_{2}} \right)=0 \\\ \end{aligned}$$ As points P and Q cannot be the same, so ${{t}_{1}}\ne {{t}_{2}}$ . Hence, we can ignore ${{t}_{1}}={{t}_{2}}$equation. So, we get $\begin{aligned} & x-2a-a\left( {{t}^{2}}_{1}+{{t}^{2}}_{2}+{{t}_{2}}{{t}_{1}} \right)=0 \\\ & x=2a+a\left( {{t}^{2}}_{1}+{{t}^{2}}_{2}+{{t}_{1}}{{t}_{2}} \right) \\\ & x=2a+a\left( {{t}^{2}}_{1}+{{t}^{2}}_{2}+{{t}_{1}}{{t}_{2}} \right) \\\ & x=2+a\left( {{t}^{2}}_{1}+{{t}^{2}}_{2}+{{t}_{1}}{{t}_{2}} \right) \\\ \end{aligned}$ Add and subtract ${{t}_{1}}{{t}_{2}}$to the bracket of right hand side of the above question. We get $\begin{aligned} & x=2+\left( {{t}^{2}}_{1}+{{t}^{2}}_{2}+{{t}_{1}}{{t}_{2}}-{{t}_{1}}{{t}_{2}} \right)a \\\ & x=2+\left( {{t}^{2}}_{1}+{{t}^{2}}_{2}+2{{t}_{1}}{{t}_{2}}-{{t}_{1}}{{t}_{2}} \right)a \\\ \end{aligned}$ $x=2+a\left( {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-{{t}_{1}}{{t}_{2}} \right)$…………… (vii) Now, divide the equations (v) by ${{t}_{1}}$and equation (vi) by ${{t}_{2}}$, we get $x+\dfrac{y}{{{t}_{1}}}-2a-a{{t}_{1}}^{2}=0$ …………… (viii) $x+\dfrac{y}{{{t}_{2}}}-2a-a{{t}_{2}}^{2}=0$……………. (ix) Now, subtract it to get value of ‘y’, so, we get $\begin{aligned} & \left( x+\dfrac{y}{{{t}_{1}}}-2a-a{{t}_{1}}^{2} \right)-\left( x+\dfrac{y}{{{t}_{2}}}-2a-a{{t}_{2}}^{2} \right)=0 \\\ & \dfrac{y}{{{t}_{1}}}-\dfrac{y}{{{t}_{2}}}-a{{t}_{1}}^{2}+a{{t}_{2}}^{2}=0 \\\ & y\left[ \dfrac{{{t}_{2}}-{{t}_{1}}}{{{t}_{1}}-{{t}_{2}}} \right]-a\left( {{t}_{1}}^{2}-{{t}_{2}}^{2} \right)=0 \\\ \end{aligned}$ Now, we know ${{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)$, so, we get $\begin{aligned} & y\left[ \dfrac{{{t}_{2}}-{{t}_{1}}}{{{t}_{1}}-{{t}_{2}}} \right]-a\left( {{t}_{1}}-{{t}_{2}} \right)\left( {{t}_{1}}+{{t}_{2}} \right)=0 \\\ & \left( {{t}_{2}}-{{t}_{1}} \right)\left[ \dfrac{y}{{{t}_{1}}{{t}_{2}}}+\left( {{t}_{1}}+{{t}_{2}} \right) \right]=0 \\\ & {{t}_{1}}-{{t}_{2}}=0,\dfrac{y}{{{t}_{1}}{{t}_{2}}}+{{t}_{1}}+{{t}_{2}}=0 \\\ \end{aligned}$ As${{t}_{2}}\ne {{t}_{1}}$ so, we get $\dfrac{y}{{{t}_{1}}{{t}_{2}}}+{{t}_{1}}+{{t}_{2}}=0$ $\dfrac{y}{{{t}_{1}}{{t}_{2}}}=-\left( {{t}_{1}}+{{t}_{2}} \right)$ $y=-{{t}_{1}}{{t}_{2}}\left( {{t}_{1}}+{{t}_{2}} \right)$……………. (x) Now, we know normal are perpendicular to each other, so, we can get an equation with the help of equation (iii) and using the normal i.e. $'-{{t}_{1}}','-{{t}_{2}}'$. So we get $$\left( -{{t}_{1}} \right)\left( -{{t}_{2}} \right)=-1$$ $${{t}_{1}}{{t}_{2}}=-1$$………….. (xi) Now, put $${{t}_{1}}{{t}_{2}}=-1$$to equation (vii) and (x), we get $\begin{aligned} & x=2+a\left( {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}+1 \right) \\\ & x=-\left( -1 \right)\left( {{t}_{1}}+{{t}_{2}} \right)=\left( {{t}_{1}}+{{t}_{2}} \right) \\\ \end{aligned}$ As, the point R is represented by coordinates by, (h, k) so, we get equations as $h=2+a\left( {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}+1 \right)$ …………… (xii) $k=\left( {{t}_{1}}+{{t}_{2}} \right)$………….. (xiii) Now, put the value of ${{t}_{1}}+{{t}_{2}}$ as ‘k’ from (xiii) to (xii). We get $$\begin{aligned} & h=2+a\left( {{k}^{2}}+1 \right) \\\ & h-2=a\left( {{k}^{2}}+1 \right) \\\ & h-2=a{{k}^{2}}+a \\\ & h-a{{k}^{2}}-2-a=0 \\\ \end{aligned}$$ Replace (h, k) by (x, y) to get locus of the point R, we get $\begin{aligned} & x-a{{y}^{2}}-2-a=0 \\\ & x=a{{y}^{2}}+2+a \\\ \end{aligned}$ **Note:** Another approach for getting normal equation would be that we can get equation of tangent by T = 0, where we need to replace $\begin{aligned} & {{x}^{2}}\to x{{x}_{1}} \\\ & {{y}^{2}}\to y{{y}_{1}} \\\ & x\to \left( \dfrac{x+{{x}_{1}}}{2} \right) \\\ & y\to \left( \dfrac{y+{{y}_{1}}}{2} \right) \\\ \end{aligned}$ So, we can write the equation of tangent through P and Q and hence, we can get slopes of them as well. So, get slopes of normal at P and Q as well, and by using $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$, we can get equations of normal are well. One may suppose P and Q as $\left( {{x}_{1}}{{y}_{1}} \right),\left( {{x}_{2}}{{y}_{2}} \right)$ and solve the problem. But it will make the solution very complex and will take more time. So, always try to solve these questions by parametric coordinates.