Question

Find the linear velocity of a point on the surface of the earth at a latitude of $60^\circ$ .
A) $\dfrac{{800}}{3}{\text{m}}{{\text{s}}^{ - 1}}$
B) $\dfrac{{800\pi }}{3}{\text{m}}{{\text{s}}^{ - 1}}$
C) $800 \times \dfrac{5}{{18}}{\text{m}}{{\text{s}}^{ - 1}}$
D) $\dfrac{{2000\pi }}{{27}}{\text{m}}{{\text{s}}^{ - 1}}$

Answer 1

The locus of all the points on the surface of the earth at a particular latitude can be considered to form a horizontal circle whose radius will be the cosine component of the radius of the earth. The earth takes 24 hours to complete one rotation in its circular orbit. The linear velocity is expressed in terms of the angular velocity of the earth’s rotation and the radius of the horizontal circle.

Formulas used:
-The linear velocity of a rotating body is given by, $v = r\omega$ where $r$ is the radius of the circle and $\omega$ is the body’s angular velocity.
-The angular velocity of a rotating body is given by, $\omega = \dfrac{{2\pi }}{T}$ where $T$ is the period of rotation.

Complete step by step answer.
Step 1: Sketch a figure depicting the latitudes of the earth. Also, express the radius of the horizontal circle corresponding to the given latitude.
The above figure depicts the horizontal circles formed by the points on the surface of the earth at different latitudes.

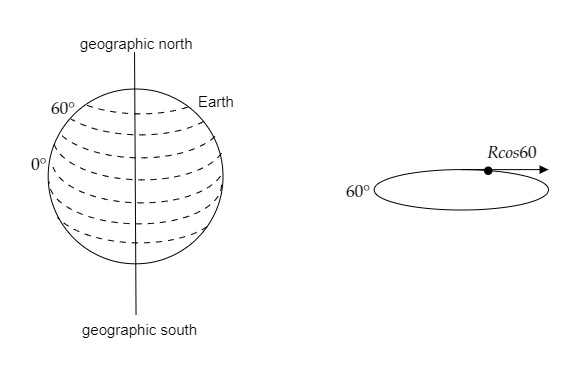
From the above figure, we have the radius of the horizontal circle as $r = R\cos \theta$
Since $\theta = 60^\circ$ we have $\cos \theta = \dfrac{1}{2}$ and the radius of the earth is taken to be $R = 6400{\text{km}}$.
Then we have the radius of the horizontal circle as $r = \dfrac{{6400}}{2} = 3200{\text{km}} = 32 \times {10^5}{\text{m}}$ .
Step 2: Express the angular velocity of the earth.
The angular velocity of a point at the given latitude can be expressed as $\omega = \dfrac{{2\pi }}{T}$ where $T$ is the period of rotation.
For earth, the period of revolution is $T = 24{\text{h}}$ .
Then we have the angular velocity as $\omega = \dfrac{{2\pi }}{{24 \times 60 \times 60}}$
Step 3: Express the linear velocity of the earth.
The linear velocity of the point on the surface of the earth at the given latitude can be expressed as $v = r\omega$ ----------- (1)
Substituting for $\omega = \dfrac{{2\pi }}{{24 \times 60 \times 60}}$ and $r = 32 \times {10^5}{\text{m}}$ in equation (1) we get, $v = \dfrac{{32 \times {{10}^5} \times 2\pi }}{{24 \times 60 \times 60}} = \dfrac{{2000\pi }}{{27}}{\text{m}}{{\text{s}}^{ - 1}}$
Thus the linear velocity of the point on earth’s surface at the given latitude is $v = \dfrac{{2000\pi }}{{27}}{\text{m}}{{\text{s}}^{ - 1}}$ .

So the correct option is D.

Note: Latitude essentially refers to the geographic north-south coordinates of a point on the surface of the earth. The east-west coordinates of the point will be provided by the longitude at that point. As the earth rotates, every point on the surface of the earth also rotates with the same angular velocity and shares the same period of revolution as that of the earth.