Solveeit Logo
Login

Question

Question: Find the lengths of the medians of the triangle with vertices \[A\left( {0,0,6} \right)\], \[B\left(...

Find the lengths of the medians of the triangle with vertices A(0,0,6)A\left( {0,0,6} \right), B(0,4,0)B\left( {0,4,0} \right)and C(6,0,0)C\left( {6,0,0} \right).

Explanation

Solution

A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side is median. Every triangle has exactly three medians, one from each vertex, and they all intersect each other at the triangle's centroid. To find the lengths of the medians of the triangle with the given vertices, we need to find the coordinates of point D, E and F then find out the lengths AD, BE and CF.

Complete step-by-step solution:
The vertices of triangle are given as:
A(0,0,6)A\left( {0,0,6} \right), B(0,4,0)B\left( {0,4,0} \right)and C(6,0,0)C\left( {6,0,0} \right)

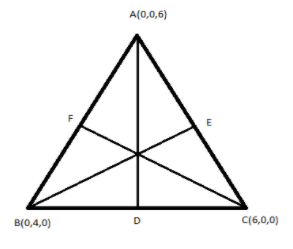
Now let us construct diagram according to the given data
Let AD, BE and CF be the medians of the given ΔABC\Delta ABC.
Since AD is the median, D is the midpoint of BC, hence the coordinates of the point D are:
⇒D=\Rightarrow D = (0+62,4+02,0+02)=(3,2,0)\left( {\dfrac{{0 + 6}}{2},\dfrac{{4 + 0}}{2},\dfrac{{0 + 0}}{2}} \right) = \left( {3,2,0} \right)
Length of AD is:
⇒AD=\Rightarrow AD = (0−3)2+(0−2)2+(6−0)2\sqrt {{{\left( {0 - 3} \right)}^2} + {{\left( {0 - 2} \right)}^2} + {{\left( {6 - 0} \right)}^2}}
⇒AD=\Rightarrow AD = 9+4+36\sqrt {9 + 4 + 36}
⇒AD=\Rightarrow AD = 49\sqrt {49}
⇒AD=7\Rightarrow AD = 7
Since BE is the median, E is the midpoint of AC, hence the coordinates of point E are:
⇒E=\Rightarrow E = (0+62,0+02,6+02)=(3,0,3)\left( {\dfrac{{0 + 6}}{2},\dfrac{{0 + 0}}{2},\dfrac{{6 + 0}}{2}} \right) = \left( {3,0,3} \right)
Length of BE is:
\Rightarrow BE =$$$\sqrt {{{\left( {3 - 0} \right)}^2} + {{\left( {0 - 4} \right)}^2} + {{\left( {3 - 0} \right)}^2}} $$ \Rightarrow BE =$$\sqrt {9 + 16 + 9} $$ \Rightarrow BE =$$\sqrt {34} $$ Since CF is the median, F is the midpoint of AB, hence the coordinates of point F are: \Rightarrow F =$$\left( {\dfrac{{0 + 0}}{2},\dfrac{{0 + 4}}{2},\dfrac{{6 + 0}}{2}} \right) = \left( {0,2,3} \right)$$ Length of CF is: \Rightarrow CF =$$\sqrt {{{\left( {6 - 0} \right)}^2} + {{\left( {0 - 2} \right)}^2} + {{\left( {0 - 3} \right)}^2}} $$ \Rightarrow CF =$$\sqrt {36 + 4 + 9} $$ \Rightarrow CF =$$\sqrt {49} $$ \Rightarrow CF = 7$

Thus, the lengths of the medians of triangle ΔABC\Delta ABC are 7, 34\sqrt {34} and 7 units.

Note: The key point to find the lengths of the triangle is that we must find the coordinates of the points, then find the lengths of the triangle. If you find the middle of any side of a triangle, you have found its midpoint. From that midpoint, you can construct a line segment to the opposite interior angle. That constructed line from the midpoint of a side to the opposite interior angle is a median.