Question

Find the length of the tangent drawn from a point whose distance from the center of a circle is 25 cm. Given that the radius of the circle is 7 cm.

Answer 1

Hint: Draw a rough figure of the tangent meeting the circle. The tangent to a circle is always perpendicular to the radius through the point of contact. You will get a right angled triangle. Solve it and find the length of the tangent drawn.

Complete step-by-step answer:

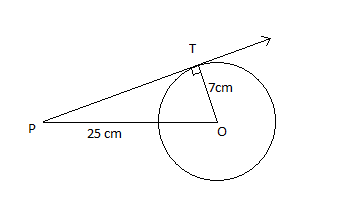
Let us consider ‘O’ as the center of the circle. Consider the figure drawn.
Let OT be the radius of the circle.
$\therefore$OT = 7 cm.
Let P be the point from which the tangent is drawn to the circle. The tangent meets at point T on the circle. Given that the length from point P to the center O of the circle is 25 cm.
$\therefore$Length of OP = 25 cm.
What we need to find is the length of PT.
From the figure, we can assume that radius OT is perpendicular to the tangent drawn, i.e. the tangent to a circle is always perpendicular to the radius through the point of contact.
$\therefore \angle OTP={{90}^{\circ }}$
Now let us consider the right angled triangle OTP.
By basic geometry we know that,
$O{{P}^{2}}=P{{T}^{2}}+O{{T}^{2}}$i.e.${{\left( hypotenuse \right)}^{2}}={{\left( altitude \right)}^{2}}+{{\left( base \right)}^{2}}$

& \therefore P{{T}^{2}}=O{{P}^{2}}-O{{T}^{2}} \\\ & PT=\sqrt{O{{P}^{2}}-O{{T}^{2}}} \\\ & PT=\sqrt{{{25}^{2}}-{{7}^{2}}}=\sqrt{625-49}=24cm \\\ \end{aligned}$$ Hence, the length of tangent from point P = 24 cm. Note: There are a lot of special properties for a tangent to a circle, like a tangent can never cross the circle. It can only touch the circle, like how we have drawn in the figure. At the point of tangency, it is perpendicular to the radius. Therefore, we took angle OTP as $${{90}^{\circ }}$$. So when you get a question related to tangents, remember both the points.