Question

Find the length of the shadow on the ground of a pole of height m when the angle of elevation $\theta$ of the sun is such that $\tan \theta = \dfrac{3}{4}$ .

Answer 1

Hint : The problem is the application of trigonometry. The value expression for $\tan \theta = \dfrac{P}{B}$ , where $P =$ perpendicular of the right triangle and $B =$ base of the right triangle.

Complete step-by-step answer :
A sun forms a shadow of a 6 meter high pole on the ground. The value of tangent of the angle of elevation of the sun is $\tan \theta = \dfrac{3}{4}$ (The figure according to the statement of the question is given below)

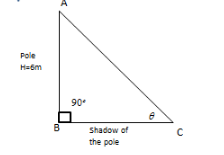
We are required to determine the shadow of the length of the pole of length B on the ground. Using the concept of trigonometry for the tangent of the angle, the value of the length of the shadow can be determined.
From the figure, In right triangle ABC,
$\tan \theta = \dfrac{{AB}}{{BC}} = \dfrac{P}{B}......(1)$
But, $\tan \theta = \dfrac{3}{4}$ (Given)
Substituting, the value of $\tan \theta = \dfrac{3}{4}$ and height of the pole AB as $H = 6{\text{ m}}$ in equation (1)
$\Rightarrow \dfrac{3}{4} = \dfrac{6}{{BC}} \\\ \Rightarrow BC = \dfrac{{6 \times 4}}{3} \\\ \Rightarrow BC = 8 \\\$
Hence, the value of the shadow of the pole formed on the ground is 8 m.

Note : The figure of the pole and its shadow on the ground should be clear in mind. Also the ratio of sides for the tangent of the angle in a right angled triangle should be clear.