Question

Find the length of the perpendicular from P(2, -3, 1) to the line $\dfrac{x-1}{2}=\dfrac{y-3}{3}=\dfrac{z+2}{-1}$.
(a) 5
(b) $\sqrt{\dfrac{531}{14}}$
(c) $\sqrt{50}$
(d) $\sqrt{\dfrac{221}{3}}$

Answer 1

First, before proceeding for this, we must assume a factor $\lambda$ which is called a proportionality factor of the given line equation. Then, by equation the given equation of line to the factor $\lambda$, we get all the points. Then, we know the condition that if the angle between the lines is ${{90}^{\circ }}$, then their dot product of direction ratios are zero. Then, by using this condition we get the value of $\lambda$and by using that we get the points. Then, by using the distance formula as $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}$, we get the desired answer.

Complete step-by-step solution:
__
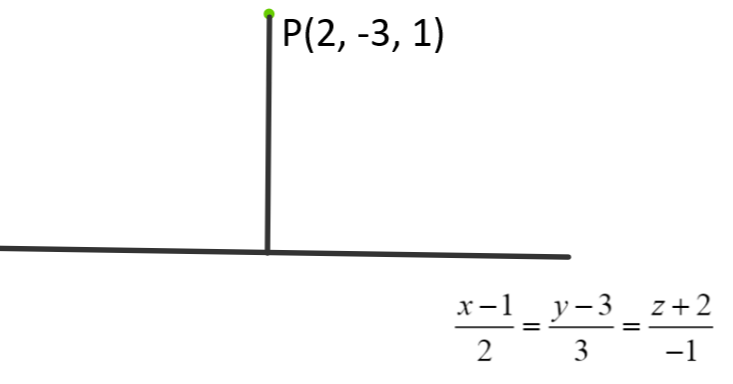
In this question, we are supposed to find the length of the perpendicular from P(2, -3, 1) to the line $\dfrac{x-1}{2}=\dfrac{y-3}{3}=\dfrac{z+2}{-1}$.
So, before proceeding for this, we must assume a factor $\lambda$which is called a proportionality factor of the given line equation.
Now, by equation the given equation of line to the factor $\lambda$, we get:
$\dfrac{x-1}{2}=\dfrac{y-3}{3}=\dfrac{z+2}{-1}=\lambda$
Then, we get the points as:
$\begin{aligned} & \dfrac{x-1}{2}=\lambda \\\ & \Rightarrow x-1=2\lambda \\\ & \Rightarrow x=2\lambda +1 \\\ \end{aligned}$
Similarly, we get for the other two conditions, the points are as:
$\left( 2\lambda +1,\text{ }3\lambda +3,\text{ }-\lambda -2 \right)$
Then, we are given with the point P(2, -3, 1) which acts like direction ratio of line which is perpendicular to the given line as:
$\begin{aligned} & \left( 2\lambda +1-2,\text{ }3\lambda +3+3,\text{ }-\lambda -2-1 \right) \\\ & \Rightarrow \left( 2\lambda -1,\text{ }3\lambda +6,\text{ }-\lambda -3 \right) \\\ \end{aligned}$
So, from the above equation, we get the direction ratios of the line by the coefficients of the factor $\lambda$ as 2, 3 and -1.
Now, we got the expression for the points of the line which is perpendicular to the given line.
So, we know the condition that if the angle between the lines is ${{90}^{\circ }}$, then their dot product of direction ratios are zero.
Then, by using this condition, we get:
$\begin{aligned} & \left( 2\lambda -1 \right)\centerdot 2+\left( 3\lambda +6 \right)\centerdot 3+\left( -\lambda -3 \right)\centerdot \left( -1 \right)=0 \\\ & \Rightarrow 4\lambda -2+9\lambda +18+\lambda +3=0 \\\ & \Rightarrow 14\lambda +19=0 \\\ & \Rightarrow 14\lambda =-19 \\\ & \Rightarrow \lambda =\dfrac{-19}{14} \\\ \end{aligned}$
Now, we will substitute the value of $\lambda =\dfrac{-19}{14}$ in the expression found as $\left( 2\lambda +1,\text{ }3\lambda +3,\text{ }-\lambda -2 \right)$ to get the points of the line as:
$\begin{aligned} & 2\left( \dfrac{-19}{14} \right)+1,\text{ 3}\left( \dfrac{-19}{14} \right)+3,\text{ }-\left( \dfrac{-19}{14} \right)-2 \\\ & \Rightarrow \dfrac{-38+14}{14},\text{ }\dfrac{-57+42}{14},\text{ }\dfrac{19-28}{14} \\\ & \Rightarrow \dfrac{-24}{14},\text{ }\dfrac{-15}{14},\text{ }\dfrac{-9}{14} \\\ \end{aligned}$
So, we get the points of the line as $\left( \dfrac{-24}{14},\text{ }\dfrac{-15}{14},\text{ }\dfrac{-9}{14} \right)$ which is perpendicular to points (1, 3, -2).
Now, we will use the distance formula to calculate the distance(d) between these points $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$and $\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ as:
$d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}$
So, by using the formula for the points found above, we get:
$\begin{aligned} & d=\sqrt{{{\left( 2+\dfrac{24}{14} \right)}^{2}}+{{\left( -3+\dfrac{15}{14} \right)}^{2}}+{{\left( 1+\dfrac{9}{14} \right)}^{2}}} \\\ & \Rightarrow d=\sqrt{{{\left( \dfrac{52}{14} \right)}^{2}}+{{\left( \dfrac{-27}{14} \right)}^{2}}+{{\left( \dfrac{23}{14} \right)}^{2}}} \\\ & \Rightarrow d=\sqrt{\dfrac{2704}{196}+\dfrac{729}{196}+\dfrac{529}{196}} \\\ & \Rightarrow d=\sqrt{\dfrac{3962}{196}} \\\ & \Rightarrow d=\sqrt{\dfrac{531}{14}} \\\ \end{aligned}$
So, the distance between the points is $\sqrt{\dfrac{531}{14}}$.
Hence, option (b) is correct.

Note: Now, to solve this type of questions we must know the angle condition of the direction ratios which is used above in the question as both the lines are perpendicular so the dot product is zero is given by the condition that:
$\cos \theta =\dfrac{\left| {{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}} \right|}{\sqrt{{{a}_{1}}^{2}+{{b}_{1}}^{2}+{{c}_{1}}^{2}}\sqrt{{{a}_{2}}^{2}+{{b}_{2}}^{2}+{{c}_{2}}^{2}}}$
Where $\left( {{a}_{1}},{{b}_{1}},{{c}_{1}} \right)$ and $\left( {{a}_{2}},{{b}_{2}},{{c}_{2}} \right)$ are the points of the line.