Question

Find the length of the perpendicular drawn from the origin to the plane $2x-3y+6z+21=0$

Answer 1

Use the fact that the perpendicular drawn from the origin to this plane is parallel to the plane’s normal vector. Observe that the vector representing this perpendicular will be a scalar multiple of the normal vector (since they are parallel). Use this to find the foot of the perpendicular lying on the plane. This point must satisfy the equation of the plane. Then use the distance formula to find the length of the perpendicular.

Complete step-by-step solution:
__
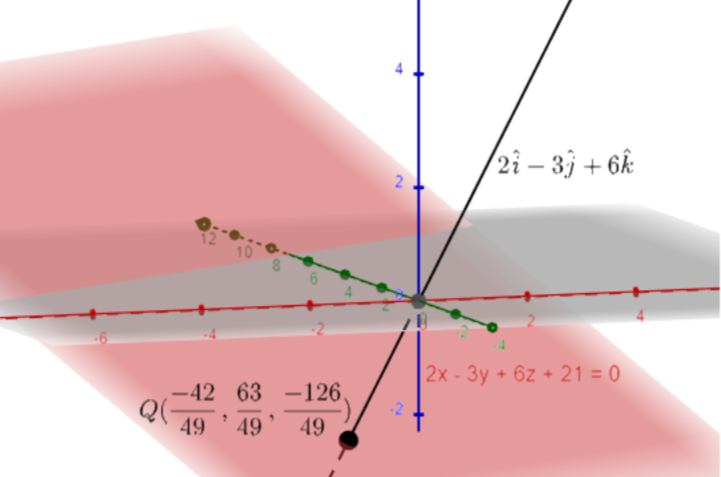
Let the point $Q\ (a,b,c)$ denote the foot of the perpendicular drawn from the origin $P\ (0,0,0)$ to the plane $2x-3y+6z+21=0$ .
We note that $\overrightarrow{PQ}=(a-0)\hat{i}+(b-0)\hat{j}+(c-0)\hat{k}=a\hat{i}+b\hat{j}+c\hat{k}$
Also, the normal vector of the given plane is $\overrightarrow{n}=2\hat{i}-3{j}+6{k}$
Since both $\overrightarrow{n}$ and $\overrightarrow{PQ}$ are perpendicular to the given plane, we see that $\overrightarrow{n}$ is parallel to $\overrightarrow{PQ}$ (i.e. $\overrightarrow{PQ}=\lambda \vec{n}$ ). Hence we obtain
$a\hat{i}+b\hat{j}+c\hat{k}=2\lambda \hat{i}-3\lambda \hat{j}+6\lambda \hat{k}$
Comparing the components on both sides, we obtain
$a=2\lambda ,\ b=-3\lambda ,\ c=6\lambda$
However, since $Q\ (a,b,c)$ lies on the given plane, it must satisfy its equation. Hence
$2a-3b+6c+21=0\Rightarrow 2(2\lambda )-3(-3\lambda )+6(6\lambda )+21=0\Rightarrow 49\lambda +21=0\Rightarrow \lambda =-\dfrac{21}{49}$
Therefore, the foot of the perpendicular drawn from the origin to the given plane is $Q\ \left( -\dfrac{42}{49},\dfrac{63}{49},-\dfrac{126}{49} \right)$ .
In the end, we use the distance formula to compute the length of this perpendicular.
$\left|\overrightarrow{PQ} \right|=\dfrac{1}{49}\sqrt{{{42}^{2}}+{{63}^{2}}+{{126}^{2}}}=\dfrac{1}{49}\sqrt{{{21}^{2}}\left( {{2}^{2}}+{{3}^{2}}+{{6}^{2}} \right)}=\dfrac{21\cdot 7}{49}=3$
Hence, the length of the perpendicular from the origin to the plane $2x-3y+6z+21=0$ is $3$.

Note: Observe how it is important to be able to identify those vectors which are perpendicular or parallel to the normal vector of the given plane and use it to your advantage. In general, the length of the perpendicular from a point $({{x}_{1}},{{y}_{1}},{{z}_{1}})$ to the plane $ax+by+cz+d=0$ could also be directly calculated by using the formula:
$d=\dfrac{\left|a{{x}_{1}}+b{{y}_{1}}+c{{z}_{1}}+d \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}$ .