Question

Find the length of the latus rectum of the parabola whose focus is the point $\left( {2,3} \right)$, and the directrix of the line $x - 4y + 3 = 0$.
A. $\dfrac{{14}}{{\sqrt {17} }}$
B. $\dfrac{{17}}{{\sqrt {17} }}$
C. $\dfrac{{15}}{{\sqrt {17} }}$
D. $\dfrac{{10}}{{\sqrt {17} }}$

Answer 1

In these type of questions where we have to find the length of the latus rectum, first we have to find the distance between the directrix of line and the focus point which can be consider variable D is given by using the formula,$D = \left| {\dfrac{{a{x_1} + b{y_1} + {c_1}}}{{\sqrt {{a^2} + {b^2}} }}} \right|$, and we have to find the length of the latus rectum of the parabola the distance must be doubled.

Complete step-by-step answer:
Given focus point is$\left( {2,3} \right)$ and equation of the directrix is given by $x - 4y + 3 = 0$,
Using the data we can draw the diagram of the parabola,

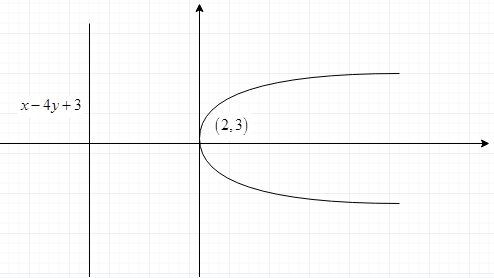
Now we have to find the length of the latus rectum, this can be found by using the distance between the directrix line and the focus point of the parabola.
Here the required distance, from the point $\left( {{x_1},{y_1}} \right)$ ,to the line $ax + by + c = 0$ is given by
This distance formula is given by $D = \left| {\dfrac{{a{x_1} + b{y_1} + {c_1}}}{{\sqrt {{a^2} + {b^2}} }}} \right|$,
Now the focus point is $\left( {2,3} \right)$, and the directrix of the line $x - 4y + 3 = 0$.
Now substituting the values in the distance formula we get,
$D = \left| {\dfrac{{(1)(2) - 4(3) + 3}}{{\sqrt {{1^2} + {{( - 4)}^2}} }}} \right|$
Now simplifying we get,
$D = \left| {\dfrac{{2 - 12 + 3}}{{\sqrt {1 + 16} }}} \right|$.
Now again simplifying we get,
$D = \left| {\dfrac{{ - 7}}{{\sqrt {17} }}} \right|$,
Now taking the absolute values we get,
$D = \dfrac{7}{{\sqrt {17} }}$,
Now we got the distance now we have to find the length of latus rectum which is twice the distance from locus to the directrix line, i.e.,
Length of the latus rectum= 2D
Length of the latus rectum=$= 2\left( {\dfrac{7}{{\sqrt {17} }}} \right)$,
$\therefore$ Length of the latus rectum $= \dfrac{{14}}{{\sqrt {17} }}$
Final Answer: The length of the latus rectum of the parabola whose focus is the point$\left( {2,3} \right)$, and the directrix of the line$x - 4y + 3 = 0$ is$\dfrac{{14}}{{\sqrt {17} }}$.

So, from the options, Option A is correct.

Note:
In these type of questions, students should know the relation between the latus rectum and the directrix of the line, which is given in formula $D = \left| {\dfrac{{a{x_1} + b{y_1} + {c_1}}}{{\sqrt {{a^2} + {b^2}} }}} \right|$ and also should remember that the length of the latus rectum is equal to twice the distance between the directrix and the focus.