Question

Find the length of the chord of the circle ${{x}^{2}}+{{y}^{2}}-10x-20y-44=0$ on the line $3x-4y=0$.

Answer 1

Hint: To find the length of the chord, we can find the endpoints of the chord which are the intersection points of the line and the circle. Then we use distance formula to find the distance between the endpoints which is nothing but the length of the chord.

Complete step-by-step answer:
In the question, it is given a circle ${{x}^{2}}+{{y}^{2}}-10x-20y-44=0$
We have to find the length of the chord on line $3x-4y=0$.

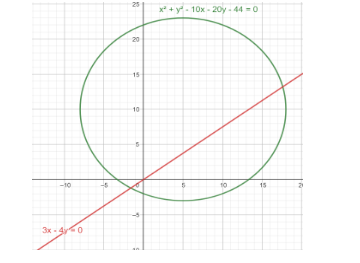
Before finding the length of the chord, we have to find the endpoints of the chords. For that we first have to find the point of intersection for line and circle. So, we have to solve the line $3x-4y=0$ with the circle ${{x}^{2}}+{{y}^{2}}-10x-20y-44=0$ .
We have the line 🡪
$3x-4y=0$
$\Rightarrow x=\dfrac{4y}{3}........\left( i \right)$
Substituting this value of $x$ from equation $\left( i \right)$ in the equation of circle, we get 🡪
${{\left( \dfrac{4y}{3} \right)}^{2}}+{{y}^{2}}-10\left( \dfrac{4y}{3} \right)-20y-44=0$
$\Rightarrow \dfrac{16{{y}^{2}}}{9}+{{y}^{2}}-\dfrac{40y}{3}-20y-44=0$
$\Rightarrow 16{{y}^{2}}+9{{y}^{2}}-120y-180y-396=0$ $\Rightarrow 25{{y}^{2}}-300y-396=0$
$\Rightarrow 25{{y}^{2}}+30y-330y-396=0$
$\Rightarrow 5y\left( 5y+6 \right)-66\left( 5y+6 \right)=0$
$\Rightarrow \left( 5y-66 \right)\left( 5y+6 \right)=0$

Hence, we get $y=\dfrac{66}{5},y=\dfrac{-6}{5}............\left( ii \right)$
From $\left( i \right)$ , we have $x=\dfrac{4y}{3}$ . Substituting both the values of $y$ from equation $\left( ii \right)$ in equation $\left( i \right)$ , we get 🡪
$x=\dfrac{4}{3}\left( \dfrac{66}{5} \right)$ and $x=\dfrac{4}{3}\left( \dfrac{-6}{5} \right)$
$\Rightarrow x=\dfrac{88}{5}$ and $x=-\dfrac{8}{5}$
So the two end points of the chords are $\left( \dfrac{88}{5},\dfrac{66}{5} \right)$ and $\left( -\dfrac{8}{5},-\dfrac{6}{5} \right)$ .
Now, before proceeding, we will discuss the distance formula from which, the distance between any two coordinate $\left( x,y \right)$ and $\left( x',y' \right)$ is given by 🡪

$d=\sqrt{{{(x-{x}')}^{2}}+{{(y-{y}')}^{2}}}.............\left( iii \right)$

Using distance formula, we can find the length of the chord joining this point. Since we have to find the distance $\left( l \right)$ between the points $\left( \dfrac{88}{5},\dfrac{66}{5} \right)$ and $\left( -\dfrac{8}{5},-\dfrac{6}{5} \right)$ , using distance formula from $\left( iii \right)$ , we get🡪
$l=\sqrt{{{\left( \dfrac{88}{5}-\left( -\dfrac{8}{5} \right) \right)}^{2}}+{{\left( \dfrac{66}{5}-\left( -\dfrac{6}{5} \right) \right)}^{2}}}$

& \Rightarrow l=\sqrt{{{\left( \dfrac{96}{5} \right)}^{2}}+{{\left( \dfrac{72}{5} \right)}^{2}}} \\\ & \Rightarrow l=\dfrac{1}{5}\sqrt{{{\left( 96 \right)}^{2}}+{{\left( 72 \right)}^{2}}} \\\ & \Rightarrow l=\dfrac{1}{5}\sqrt{9216+5184} \\\ & \Rightarrow l=\dfrac{\sqrt{14400}}{5} \\\ & \Rightarrow l=\dfrac{120}{5} \\\ & \Rightarrow l=24 \\\ \end{aligned}$$ Note:There is a possibility of error while finding the endpoints of the chords. When we substituted the two values of $ y $ in $ x=\dfrac{4y}{3} $ , we got two values of $ x $ . It is a possibility that one does not make the correct pair of $ \left( x,y \right) $ . Instead of the correct pair $ \left( \dfrac{88}{5},\dfrac{66}{5} \right) $ and $ \left( -\dfrac{8}{5},-\dfrac{6}{5} \right) $ , one may make the pair as $ \left( \dfrac{88}{5},-\dfrac{6}{5} \right) $ and $ \left( -\dfrac{8}{5},\dfrac{66}{5} \right) $ . So, one must find the coordinate $ \left( x,y \right) $ keeping in mind that $ x $ and $ y $ should be corresponding to each other.