Question

Find the length of the chord intercepted by the circle ${x^2} + {y^2} - 8x - 2y - 8 = 0$ on the line $x + y + 1 = 0$.

Answer 1

To solve this question first we express one variable of line in terms of another variable and then put that value in the equation of circle from which we are able to find one coordinate of both the variables. Then we put that coordinate in the equation of the line and find another coordinate of the same point. Now we have points with the coordinate then we use the distance formula between two points in order to find the length of the intercept.

Complete step-by-step solution:

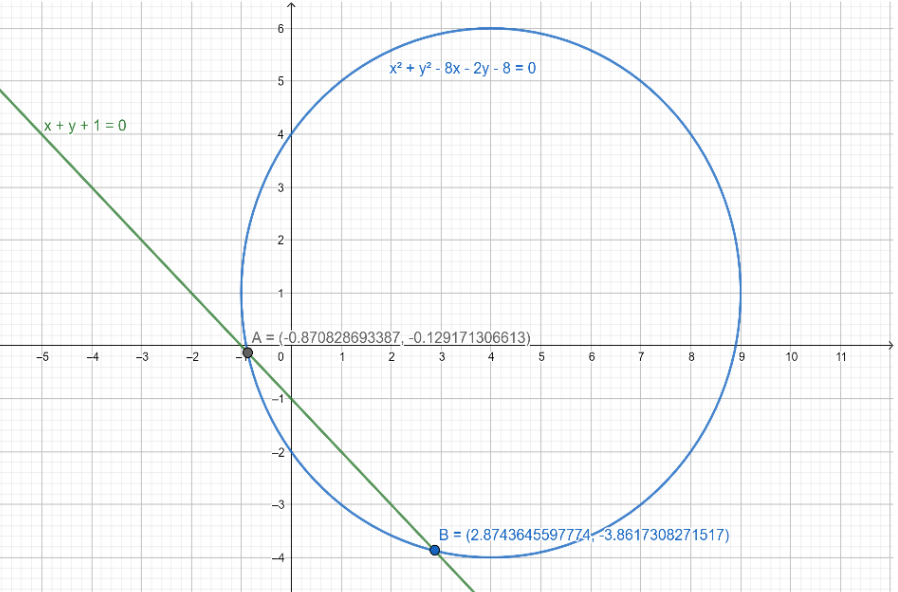
Given,
Equation of circle ${x^2} + {y^2} - 8x - 2y - 8 = 0$
Equation of the line $x + y + 1 = 0$
To find,
The length of the chord intercepted by the circle.
The equation of the line $x + y + 1 = 0$
$x = - y - 1$
On putting this value in the equation of the circle we got both the y coordinate of the intersection of the line.
On putting this value in equation of the circle
${\left( { - y - 1} \right)^2} + {y^2} - 8\left( { - y - 1} \right) - 2y - 8 = 0$
On further solving
${y^2} + 1 + 2y + {y^2} + 8y + 8 - 2y - 8 = 0$
On adding all the like terms
$2{y^2} + 8y + 1 = 0$
Now use the formula of finding the roots of the quadratic equation
$roots = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$
Here, $a$ is the coefficient of ${y^2}$ $a = 2$
$b$ is the coefficient of $y$ $b = 8$
$c$ is the constant term $c = 1$
On putting all these values in formula
$roots = \dfrac{{ - 8 \pm \sqrt {{8^2} - 4 \times 2 \times 1} }}{{2 \times 2}}$
On further calculations
$roots = \dfrac{{ - 8 \pm \sqrt {64 - 8} }}{4}$
$roots = \dfrac{{ - 4 \pm \sqrt {14} }}{2}$
The $y$ coordinates of the intercept are ${y_1}$ and ${y_2}$
${y_1} = \dfrac{{ - 4 + \sqrt {14} }}{2}$
${y_2} = \dfrac{{ - 4 - \sqrt {14} }}{2}$
On putting the value of y intercept in equation of line then we get the value of x intercept
$x = - y - 1$
On putting the value of ${y_1}$ we get the value of ${x_1}$
${x_1} = - \left( {\dfrac{{ - 4 + \sqrt {14} }}{2}} \right) - 1$
On further solving
${x_1} = \dfrac{{ + 4 - \sqrt {14} - 2}}{2}$
${x_1} = \dfrac{{2 - \sqrt {14} }}{2}$
On putting the value of ${y_2}$ we get the value of ${x_2}$
${x_2} = - \left( {\dfrac{{ - 4 - \sqrt {14} }}{2}} \right) - 1$
On further solving
${x_2} = \dfrac{{ + 4 + \sqrt {14} - 2}}{2}$
${x_2} = \dfrac{{2 + \sqrt {14} }}{2}$
Here we got the coordinates of both the points
$a = \left( {{x_1},{y_1}} \right)$
$a = \left( {\dfrac{{2 - \sqrt {14} }}{2},\dfrac{{ - 4 + \sqrt {14} }}{2}} \right)$
$b = \left( {{x_2},{y_2}} \right)$
$a = \left( {\dfrac{{2 + \sqrt {14} }}{2},\dfrac{{ - 4 - \sqrt {14} }}{2}} \right)$
Now we have to find the length of the intercept and we know the coordinates of the line.
$d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
On putting the values
$d = \sqrt {{{\left( {\dfrac{{2 + \sqrt {14} }}{2} - \dfrac{{2 - \sqrt {14} }}{2}} \right)}^2} + {{\left( {\dfrac{{ - 4 - \sqrt {14} }}{2} - \dfrac{{ - 4 + \sqrt {14} }}{2}} \right)}^2}}$
On further solving
$d = \sqrt {{{\left( {\dfrac{{2\sqrt {14} }}{2}} \right)}^2} + {{\left( {\dfrac{{ - 2\sqrt {14} }}{2}} \right)}^2}}$
On canceling the same term from numerator and denominator.
$d = \sqrt {14 + 14}$
Final answer:
The length of the intercept by the circle on the line is
$\Rightarrow d = \sqrt {28}$

Note: It may be possible that the question asks us to find only the coordinates of the intersected points of the line and the circle. Students commit mistakes in many places like they put the value of y in the equation of a circle and it may be possible that we are unable to solve that quadratic equation.