Question

Find the length of the arc in terms of $\pi$ that subtends an angle of ${{30}^{o}}$ at the center of a circle of radius 4 cm.

Answer 1

Hint: First of all convert ${{30}^{o}}$ in radians by multiplying it by $\dfrac{\pi }{180}$. Then use the formula for the length of arc which subtends angle at the center, $\theta =R\theta$ where R is the radius of the circle and $\theta$ is in radians.

Here, we are given a circle of radius 4 cm in which an arc subtends an angle of ${{30}^{o}}$ at the center. We have to find the length of this arc in terms of $\pi$.

First of all, we must know that an arc of a circle is a portion of the circumference of the circle. The length of the arc is simply the length of its portion of circumference. Also, the circumference itself can be considered a full circle arc length.

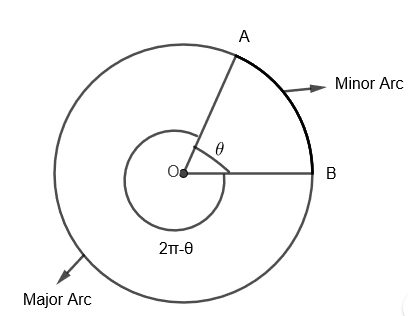
We have two types of arc between any two points in a circle. One is the major arc and other is the minor arc. We know that the total angle at the center of the circle is $2\pi$. Here, the shorter arc made by AB which subtends angle $\theta$ at the center of the circle is a minor arc. Then, the longer arc made by AB which subtends angle $\left( 2\pi -\theta \right)$ at the center of the circle is the major arc.

Here, as we can see, $\left( 2\pi -\theta \right)>\theta$.

Now, we know the circumference of the circle $=2\pi R$, where R is the radius of the circle.
We know that circumference is also an arc of full circle arc length. Therefore, we can say that the length of the arc made by $2\pi$ angle = $2\pi R$.

By dividing $2\pi$ on both sides, we get the length of the arc made by unit angle = R.
By multiplying $\theta$ [in radian] on both sides, we get, length of the arc made by $\theta$ angle $=R\theta ....\left( i \right)$.
Now, we have to find the length of the arc which subtends an angle of ${{30}^{o}}$ at the center.

We can show it diagrammatically as follows,

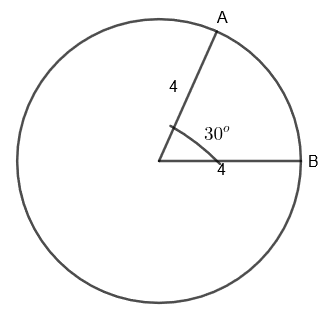
Here, we have to find the length of minor arc AB. As we have to find the length in terms of $\pi$, we will first convert ${{30}^{o}}$ into radians.

We know that, to convert any angle from degree to radians, we must multiply it by $\dfrac{\pi }{180}$,
So, we get ${{30}^{o}}=30\times \dfrac{\pi }{180}\text{radians}$
By simplifying, we get
${{30}^{o}}=\dfrac{\pi }{6}\text{radians}$
Now, to find the length of arc subtended by $\dfrac{\pi }{6}$ angle,
We will put $\theta =\dfrac{\pi }{6}$ and R = 4 cm in equation (i), so we get,
Length of the arc made by $\dfrac{\pi }{6}$ radian angle $=\dfrac{\pi }{6}\times 4cm$
$=\dfrac{2\pi }{3}cm$
Therefore, we get the length of the arc which subtends an angle of ${{30}^{o}}$ at the center of the circle in terms of $\pi$ as $\dfrac{2\pi }{3}cm$.

Note: Students can also find the length of the arc directly by remembering the following formulas.
Length of arc = $R\theta$ when $\theta$ is in radian and length of arc $=\dfrac{R\theta \pi }{{{180}^{o}}}$ when $\theta$ is in degrees.
Also, students must properly read if the major or minor arc is asked in question and use $\theta$ accordingly.