Question

Find the length of major axis, minor axis, latus rectum and eccentricity of the ellipse $9{{x}^{2}}+16{{y}^{2}}=144$. $$$$

Answer 1

We convert the given equation $9{{x}^{2}}+16{{y}^{2}}=144$ of ellipse by dividing 144 into the standard form $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ and obtain $a,b$. We find the length of major axis, minor axis, latus rectum and eccentricity using the expression in $a,b$ as $2a,2b,\dfrac{2{{b}^{2}}}{a},\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$respectively.$$$$

Complete step by step answer:
We know that the ellipse is the locus of a point which moves with the condition that the sum of distances from two other points is constant. Two other points are called focal points say ${{F}_{1}},{{F}_{2}}$ or foci and the midpoint of the foci is called centre say O. The longest chord that joins the foci is called major axis and the chord perpendicular to major axis passing through the centre is called minor axis. The endpoints of major axis say ${{V}_{1}},{{V}_{2}}$ and end points of minor axis say ${{V}_{3}},{{V}_{4}}$ are called vertices of the ellipse. The chord perpendicular to the major axis passing through any of the foci ${{F}_{1}},{{F}_{2}}$ is called latus rectum. Eccentricity is parameter define the degree of elongation of ellipse and is the ratio of semi-focal length $O{{F}_{1}}=O{{F}_{2}}$ to semi-major axis $O{{V}_{1}}=O{{V}_{2}}$.
The standard equation of ellipse in Cartesian from assume that origin as the centre $O\left( 0,0 \right)$ and the major axis lying on $x-$axis with foci ${{F}_{1}}\left( -c,0 \right),{{F}_{2}}\left( c,0 \right)$ ,vertices on major axis ${{V}_{1}}\left( -a,0 \right),{{V}_{2}}\left( a,0 \right)$ and vertices on minor axis ${{V}_{3}}\left( 0,b \right),{{V}_{4}}\left( 0,-b \right)$. The rough figure of standard ellipse is given below. $$$$

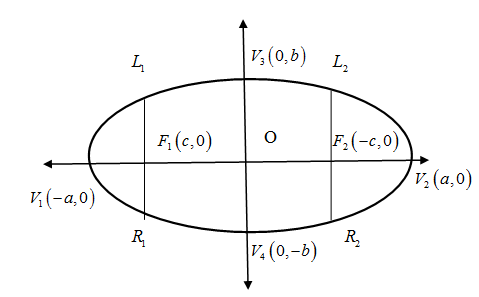
The latus rectums in the above diagram are ${{L}_{1}}{{R}_{1}},{{L}_{2}}{{R}_{2}}$.The equation of ellipse in standard form is given by
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
We know that the length of major axis, minor axis , latus rectum and eccentricity is given by ${{V}_{1}}{{V}_{2}}=2a,{{V}_{3}}{{V}_{4}}=2b,{{L}_{1}}{{R}_{1}}={{L}_{2}}{{R}_{2}}=\dfrac{2{{b}^{2}}}{a},e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$ respectively.
We are given in the question the equation of ellipse,
$9{{x}^{2}}+16{{y}^{2}}=144$
Let us convert it into the standard form by dividing both sides of the above equation by 144. We get,

& \dfrac{9{{x}^{2}}}{144}+\dfrac{16{{y}^{2}}}{144}=\dfrac{144}{144} \\\ & \Rightarrow \dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1 \\\ & \Rightarrow \dfrac{{{x}^{2}}}{{{4}^{2}}}+\dfrac{{{y}^{2}}}{{{3}^{2}}}=1 \\\ \end{aligned}$$ We compare the above equation of ellipse with the standard equation to ellipse to get $a=4,b=3$.  **So the length of major axis, minor axis, latus rectum and the eccentricity of the given ellipse are $$\begin{aligned} & {{V}_{1}}{{V}_{2}}=2a=2\times 4=8 \\\ & {{V}_{3}}{{V}_{4}}=2b=2\times 3=6 \\\ & {{L}_{1}}{{R}_{1}}={{L}_{2}}{{R}_{2}}=\dfrac{2{{b}^{2}}}{a}=\dfrac{2\times {{3}^{2}}}{4}=4.5 \\\ & e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}=\sqrt{1-\dfrac{{{3}^{2}}}{{{4}^{2}}}}=\sqrt{\dfrac{16-9}{16}}=\dfrac{\sqrt{7}}{4} \\\ \end{aligned}$$** **Note:** We can obtain the coordinates of the foci as ${{F}_{1}}\left( -ae,0 \right),{{F}_{2}}\left( ae,0 \right)$. We note that the standard equation assumes that $a > b $ as in the problem but if we have $b > a $ then the major axis will lie on the $y-$axis. We must be careful of the confusion of formula of ellipse from hyperbola whose major axis, minor axis, latus rectum is same as ellipse but the eccentricity of hyperbola is $e=\sqrt{1+\dfrac{{{b}^{2}}}{{{a}^{2}}}}$. We have rejected negative square roots for $e$ as eccentricity is always positive.